| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 강화학습
- selenium
- 빅데이터
- dropout
- 불확실성
- Graph
- 텍스트마이닝
- uncertainty
- VAE
- PYTHON
- 알고리즘
- 크롤링
- 논문리뷰
- 리눅스
- 코딩테스트
- pandas
- YarinGal
- R
- GNN
- 베이지안
- Crawling
- DATA
- bayesian
- pytorch
- 우분투
- 데이터분석
- AI
- 백준
- 텍스트분석
- 파이썬
- Today
- Total
끄적거림
[논문 리뷰] PRIORS IN BAYESIAN DEEP LEARNING: A REVIEW 본문
cold posterior 관련 논문을 찾다가 발견한 리서치? 느낌의 논문이라 볼 수 있다.
이 paper에는 cold posterior의 내용이 아주 잠깐 스쳐 지나가게 나오긴 하지만, 베이지안의 철학을 이어받는 논문이라 볼 수 있다.
스위스 취리히 대학의 CS학과에서 작성되었으며, 2021년 NeurIPS의 Bayesian Deep Learning 워크샵에 게재된 내용이다.
해당 워크샵에서 한해의 베이지안에 대해 전반적으로 다루고 있으니 베이지안에 관심이 있으신 분들이면 한 번쯤 사이트에 접속해보길 권해드린다.
논문 링크 : https://arxiv.org/pdf/2105.06868.pdf
0. Abstract
While the choice of prior is one of the most critical parts of the Bayesian inference workflow, recent Bayesian deep learning models have often fallen back on vague priors, such as standard Gaussians.
Bayesian Inference에서 가장 중요한 부분 중 하나는 prior를 선택하는 것이지만, 최근 Bayesian Deep Learning model들은 standard Gaussian과 같은 모호한 prior를 적용하는 퇴보하는 모습을 보여주고 있다.
In this review, we highlight the importance of prior choices for Bayesian deep learning and present an overview of different priors that have been proposed for (deep) Gaussian processes, variational autoencoders, and Bayesian neural networks.
이 review에서는 Bayesian Deep Learning에서 prior 선택의 중요성을 강조하고, 이를 Gaussian Process(이하 G.P.), Variational AutoEncoder(이하 VAE), Bayesian Neural Network(이하 BNN)에서 각기 다른 prior를 적용하는 overview를 하고자 한다.
We also outline different methods of learning priors for these models from data.
위의 모델들에 대해 data로부터 prior를 학습하는 다른 method를 보여줬다.
We hope to motivate practitioners in Bayesian deep learning to think more carefully about the prior specification for their models and to provide them with some inspiration in this regard.
이번 기회를 빌어 여러 model을 학습하는 사람들에게 prior를 잘 선택하는 것이 중요하다는 것을 알려주려 한다.
1. Introduction
1.1
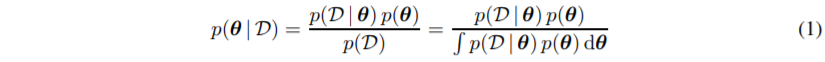
Bayes rule에 대해 일반적인 개념을 설명하고 있다.
이미 너무 유명하고 익숙하고 기본적인 개념이기 때문에 넘어가겠다.
1.2

1.1에서 Bayes Rule에 대한 설명이 나오던 중 hyperparameter라는 개념이 나오는데, 쉽게 말하면, prior에 대한 prior라고 보면 된다.
예를 들어, 우리가 구하고자하는 parameter $\theta$가 있고, 이 $\theta$의 prior가 Normal distribution을 따른다면, Normal distribution의 parameter인 평균(mean)이 또 다른 분포를 따르는 것을 의미한다.
1.3

이 식은 posterior predictive에 대한 설명이다.
쉽게 정리하자면, 어떻게 꾸역꾸역 posterior를 구했으면, posterior를 이용하여 실질적으로 예측을 위한 예측 분포를 구하는 과정이다.
이러한 과정을 통하여 결국엔 posterior density를 구하는 것이 최종 목적이긴 하다.
1.4
그러나 실제로는 최적의 prior를 선택하는 것을 objective prior, empirical Bayes 혹은 두 개의 조합으로 하는 등, prior 구하는 것을 간단히 하고, 다소 성가신 일로 치부해 왔다.
특히 Bayesian Deep Learning에서 Standard Gaussian과 같은 의미없는 prior를 구하는 것이 흔히 발생되고 있다.
내가 여태껏 봐왔던 논문들도 그냥 별 이유 없이 prior를 Standard Gaussian로 잡고 시작한다.
왜냐하면 Standard Gaussian이 가장 자연계에서 흔한 분포에다가 Standard Gaussian이 갖는 특징이 계산을 할 때 너무 편하기 때문이다.
이 이외의 이유로 Standard Gaussian을 쓰는 경우는 별로 보지 못했다.
1.5
이렇게 prior를 선택하는 것에 대해 깊게 고민하지 않는 trend는 문제가 될 수 있다.
왜냐하면, Bad prior를 고르면 inference를 할 때 안좋은 결과를 도출하기 때문이다.
일단, 정보가 없는 혹은 정보가 부족한 prior를 선택하는 것은 Bernstein-von-Mises 이론의 asymptotic consistency guarantees에 충족되지 않기 때문에, 실제로 많이 사용되는 이론은 아니다.
게다가 실제 practical inference의 non-asymptotic 체계에서 prior는 posterior에 강한 영향을 미칠 수 있고, 확률을 parameter space에서 임의의 sub-space로 보내버릴 수 있다.
1.6
prior를 잘못 선택하는 것은 Bayesian Inference를 사용하기 위해서 억지로 prior를 끼워 맞추는 것과 같다.
예를 들면, prior를 잘못 정하면 marginal density $P( y | \theta )$가 의미 없게 되기도 한다.
그렇게 되면 Bayesian Model을 선택할 때 최적의 model을 선택할 수 없다.
1.7
prior를 잘못 선택하는 것이 필연적으로 최적의 성능을 내기 위해 posterior를 tempering하는 것이다.
그렇기 때문에 posterior를 tempering하는 것이 요즘 Bayesian Deep Learning model에서는 실험적으로 필요한 것이다.
이 부분에서 매우 큰 깨달음을 얻었다.
기존에 내가 cold posteior에 대한 최신 논문과 article들을 살펴보면서 이론적, 수학적인 뒷받침 근거가 좀 부족하고, 실험적으로, 혹은 경험적으로 성능이 더 좋았다더라 하는 결과를 많이 보았다.
그 때문에 다른 논문이나 article에서는 cold posteir에 대한 부정적인 견해와 지적이 나오기도 하지만, posterior를 tempering 하는 것이 어쨌든 성능이 좋아지기는 하기 때문에 각광을 받고 있었다.
본 paper에서는 성능 개선을 위해서 posterior tempering으로 발전할 수 밖에 없었다는 것을 지적하고 있다.
성능이 좋지 못한 원인을 posterior에서 찾을 것이 아니라 prior에서 찾자는 것이 본 논문의 핵심이다.
2. Prior in (Deep) Gaussian Process(이하 G.P.)
G.P.에 대한 일반론과 prior 관점에서 내용을 전달하고 있지만 일단은 지금은 패스하고, VAE부터 보겠다.
3. Prior in Variational AutoEncoder(이하 VAE)
서두에는 VAE의 일반론에 대해서 설명하고 있다.
- 계산 불가능한 posterior를 정확히 inference하기 위한 NN의 non-linearity 때문에, variational density인 $q(z|x)$로 근사한다.
- variational density를 구하기 위한 ELBO 설명
3.1 Distributional VAE priors
3.1.1
해당 절에서는 distributional prior라는 개념을 사용하는데, 이 것은 standard VAE에서 $q(z)$를 지칭하는 용어로써 사용된다.
기존에 우리가 알고 있는 latent variable의 분포라고 생각하면 된다.
그런데 여기에다가 variational posterior인 $q(z|x)$ 의 form으로 변경하는 것이 prior를 fitting하는데 더 좋다고 한다.
3.1.2

일단 이것은 vMF prior인데, d dimentional latent space이고, 평균인 $\mu$, concentration parameter인 $\kappa$, 그리고 $I_k$는 수정된 Bessel function이라고 한다.
이 $p(z)$ distribution은 3차원 이상의 구모양(hyperspherical)의 Multivariate Gaussian distribution처럼 보인다.
그러나 이 $p(z)$의 단점중 하나는 Bessel function이 closed form으로 general하게 계산할 수 없기 때문에 numerically approximation을 해야한다는 것이다.
이런 hyperspherical prior는 standard Gaussian data에 비해 benchmark 데이터에서의 VAE 성능을 더 향상시키지만, 사실 low-dimensional latent space에서 향상되었던 것이다.
3.1.3

수정된 Bessel function의 numerical issue를 해결하기 위해서 power-spherical distribution을 vMF을 위해 대체재로 제안했다.
$\mu$가 평균이고, $\kappa$가 concentration parameter이고, $\Gamma(\dot)$은 Gamma function이다.
여기서는 Bessel function보다는 $\Gamma(\dot)$을 사용하는데, $\Gamma(\dot)$이 Bessel function보다 evaluation하기에 쉽기 때문에 결국 power-spherical distribution이 closed-form으로 evaluation하기 수월하다.
또한, 모수적 sampling을 하기에도 좋다고 한다.
실험적으로는 vMF prior를 사용할 때 VAE에서 비슷한 성능을 내었고, numerically 더 stable하다고 한다.
3.1.4

또 다른 prior로는 Mixture Gaussian인데, weighted된 Mixture Gaussian이다.
$p(z)$는 $k$개의 Gaussian으로 Mixing되기 때문에 k-dim이고, weight는 일단 $\frac{1}{k}$로 동일하게 적용된다.
이러한 방법론은 latent space에서 disjoint하게 clustering하는 것에서 영감을 받았다고한다.
그러나 다른 clustering method와 마찬가지로 cluster 갯수인 $k$를 정하는 것에 대한 issue가 있다.
이 문제는 stick-breaking이나 Dirichlet process hyper prior와 같은 방법으로 최적화 할 수 있다.
물론 cost가 inference하는데 더 소요되긴 한다.
3.1.5

만일 data point들 사이의 potential similarity에 대해 prior knowledge가 있다면, 그리고 우리가 그것을 kernel function으로 생각할 수 있다면, G.P.는 VAE에서 강력한 prior가 될 수 있다.
$Z=(z_1, ..., z_n)$을 latent variable matrix라 하고, $K_{zz}$를 kernel matrix라고 한다.
G.P.를 prior하는 model은 conditional generalization, time series, missing data imputation, disentanglement에서 유리하게 작용한다.
하지만 이 model들은 standard VAE에 비해 더 많은 computational cost가 발생한다.
kernel matrix의 inverse를 구하기 위해 $O(n^3)$정도의 계산복잡도가 소요된다.
그러나 이 연산은 줄일 수 있을 뿐 아니라, generative process의 prior에 의하면, 추가적인 G.P. prior나 tensor값을 갖는 prior로 확장하여 사용할 수 있다.
3.2 Structural VAE priors
3.2.1
이 절에서는 바로 위에서 논의했던 distributional prior와는 다른게 VAE model의 실질적인 prior distribution $p(z)$를 바꾸는 것 뿐만 아니라, model 자체를 바꿀 수 있는 structural prior를 사용한다.
어떻게 보면 위의 distributional prior의 확장판이다.
예를 들어, 앞에서 언급한 Gaussian Mixture prior는 각 factor가 latent mixture component에 의존하는 mixture-of-decoder, 즉, factorized generative likelihood로 확장할 수 있다.
또 다른 예로는 G.P. prior가 있는데, latent dataset $z$ 전체를 정의하기 때문에 $X$를 jointly encoding하는 수정된 encoder의 장점을 갖는다.
3.2.2

이런 수정된 아키텍쳐를 갖는 distributional prior에 더하여, standard VAE 아키텍쳐를 인식하지 못하는 structured prior가 있다.
그 예로 위 그림처럼 hierarchical prior가 있다.
하나의 latent variable $z$를 갖는 것 대신에, 위 수식처럼 서로 hierarchical하게 depend하는 k개의 다른 latent variables ${z_1, ... , z_k}$를 갖는다.
이런 model은 17번 수식에서 조건부확률을 parameterize하기 위한 generative feature를 갖는 model data를 더 좋게 만들고, VAE를 사용하는 image generation에서 SOTA급을 찍었다고 한다.
3.2.3

또 다른 structural prior는 VQ-VAE prior와 같은 discrete latent prior이다.
$E$는 prototye의 finite dictionary이고, $z_e$는 continuous latent variable이다.
중요한 것은 continuous한 $z_e$를 두는 것이 아니라, dictionary $E$에 대한 uniform prior로 부르는 discrete한 $z_q$를 두는 것이다.
이런 discrete한 latent variable은 low cost로 save할 수 있기 때문에 standard VAE보다 압축성이 좋다.
위에서 설명한 hierarchical latent variable과 이 discrete한 latent variable을 같이 사용할 때 경쟁력있는 image generation 성능에 도달할 수 있다고 한다.
게다가, discrete latent variable은 Self-Organization Map(이하 SOM)과 같이 주변의 structure을 포함하도록 확장할 수 있다.
