| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- selenium
- Graph
- DATA
- GNN
- 텍스트마이닝
- pandas
- AI
- 강화학습
- 알고리즘
- 베이지안
- 데이터분석
- 텍스트분석
- 빅데이터
- 크롤링
- PYTHON
- 코딩테스트
- pytorch
- bayesian
- Crawling
- uncertainty
- 백준
- 파이썬
- 우분투
- 불확실성
- R
- 리눅스
- YarinGal
- VAE
- 논문리뷰
- dropout
- Today
- Total
끄적거림
[논문 리뷰] (정리중) Stochastic gradient Markov chain Monte Carlo - 2.Background 본문
[논문 리뷰] (정리중) Stochastic gradient Markov chain Monte Carlo - 2.Background
Signing 2022. 1. 17. 21:32[논문 소개] Stochastic gradient Markov chain Monte Carlo
[논문 리뷰] Stochastic gradient Markov chain Monte Carlo - 1.Introduction
이번 시간에는 본격적인 이론에 관련된 내용을 다뤄보겠다.
그러기 위해서는 미리 알아야하는 개념들이 있는데 논문 순서대로 짚어보고 넘어가자.
2. Langevin-based Stochastic Gradient MCMC
이번 절에서는 SG-MCMC의 기초로서 Langevin diffusion과 discrete-time approximation를 소개한다.
또한 posterior approximation에 대한 이론적 오류 한계와 Gaussian에서 Stochastic gradient Langevin dynamics의 예시를 제시한다.
2.1 The Langevin Diffusion
우리는 우리가 원하는 target density $ \pi(\theta) $로부터 sampling하기를 원한다.
($\theta$는 d-dim이고, unnormalized density이다.)

(1)번 식은 target density를 나타낸 것인데, 그 중에서 $U(\theta)$ 함수를 potential function이라고 한다.
이 potential function은 연속이며, 미분가능한 함수이다.
본 논문에서 이 함수가 가장 중요하다 해도 과언이 아니라고 하니 잘 살펴보자.
(cold posterior에서도 핵심이 되는 함수이다.)
일단, 빅데이터를 위한 Bayesian Analysis에서 착안을 했는데, potential이라고 하는 것은 data point를 모두 합한 것이라고 정의할 수 있다.
예를 들어, 우리가 independent한 data인 $y_1, y_2, ... y_N$을 가지고 있다면,
$$ \pi(\theta) ~ \propto ~ p(\theta) \prod_{i=1}^N f(y_i|\theta) $$
라는 $\pi(\theta)$에 대한 수식을 정의할 수 있는데, 이 때 $p(\theta)$는 prior density이고, $f(y_i|\theta)$는 $i$번째 데이터에 대한 likelihood이다.
위와 같이 세팅했다면 우리는 아래와 같은 식을 유도할 수 있다.
$$ U(\theta) = \sum_{i=1}^N U_i(\theta) = \sum_{i=1}^N (-log f(y_i|\theta) - (1/N)log p(\theta)) $$
우리가 원하는 target 분포를 어쨌든 정의하긴 했다.
여기서 직접적인 분포를 구하기 어려우니 일단 target density로부터 sampling을 해야할텐데, 그 중에 한 가지 방법이 바로 $\pi$를 고정된 distribution이라고 가정하고 stochastic process를 시뮬레이션하는 것이다.
이런 process로 sampling을 꽤 오래한다고 하면, 처음 우리가 generate했던 sample들은 버린다.

이해를 돕기 위해 사진을 가져왔다.
x축은 iteration이라고 생각하면 될 것 같고, y축은 stochastic process를 시뮬레이션하면서 얻은 sample point라고 해보자.
-> 위에서 말했던 처음 generate했던 sample을 버린다는 말은 그림에서 앞에 회색으로 음영된 부분을 버린다는 것을 의미하고, 이렇게 앞의 sample을 버리는 행위를 `burn-in` 이라고 표현한다.
burn-in 하는 이유는 일단 sampling하면서 처음 sample들은 원하는 분포를 찾아가는 과정에서 나온 것이므로, 많은 error가 존재할 가능성이 크기 때문이다.
버리고 난 뒤 나머지 뒤의 sample들은 $\pi$를 근사하는 것으로 여길 수 있다.
이렇게 approximation한 것의 quality는 얼마나 빠르게 고정된(더 이상 변하지 않는) 분포로 수렴하는가에서 결정된다.
-> 이 말은 위 사진에서 노란색 음영된 부분처럼 일정 분포로 얼마나 빠르게 수렴하는가를 의미한다.
여기까지는 흔히 MCMC나 Metropolis와 같은 sampling 방법론에서 흔히 볼 수 있는 것이니 쉽게 넘어갈 수 있다.
다음 내용으로 넘어가기 전에 미리 알아야할 개념이 있다.
참고 링크1, 참고 링크2에 자세히 나와있지만 낯선 개념과 용어들이 즐비하다.
Stochastic Process
번역하면 "확률 과정"으로 말 할 수 있고, Dropout as a Bayesian 논문 리뷰에서도 다뤘던 random process와 닮은 구석이 있다.
기본적으로 Stochastic Process는 시간을 index로 두고 있고, 시간에 따라 분포가 변경되는 것을 의미한다.
Brownian Motion
경제학, 특히, 주식과 같은 현상을 두고 볼 때 사용되는 개념으로, 물리학에서 아이슈타인의 업적인 브라운 운동과 같은 용어를 사용하고 있다. 여기서 말하는 브라운 운동은 stochastic process가 4가지 조건을 만족할 경우 브라운 운동이라고 정의하고 있다.
1. Z(0) : Stochastic Process의 출발 위치는 0이다.
2. Z(t)-Z(0) ~N(0, t) : Stochastic Process의 0시점부터 t 시점까지 변화된 양은 평균이 0이고, 분산이 t인 정규분포를 따른다.
3. 각 구간이 서로 겹치지 않으면 각 구간마다 변화된 Stochastic Process의 양은 서로 독립이다.
4. Z(t)는 연속형이지만, 거의 모든 점에서 미분 불가능하다.
특히, Brownian Motion을 기초로 하는 임의의 Stochastic Process의 Stochastic Differential Equation은 아래와 같이 일반화가 가능한데,
$$ dX(t) = \alpha(X(t), t) * dt + \sigma(X(t), t) * dZ(t) $$
이 때, $\alpha(X(t), t)$를 결정론적인 part라하며 drift term이라고 하고, $\sigma(X(t), t)$를 확률론적인 part라 하며 diffusion term이라고 한다.
일반적인 Langevin diffusion에서는 stochastic differential 방정식을 아래와 같이 정의한다.
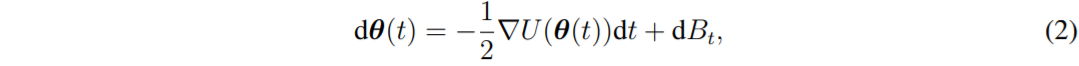
여기서 $ \nabla U(\theta(t))$ 는 drift term이고, $B_t$는 $\pi$라는 고정된 분포를 갖는 $d$-dimension에서의 브라운 운동이다.
(drift term 이라는 것)
(애초에 Langevin diffusion이라는 개념이 물리통계학에서 나오는 개념이다.)
위 (2) 수식은 아주 작은 시간을 interval로 두는 continuous-time Markov process의 dynamics(이하 역학이라 표기하겠음.)으로 정의하여 해석할 수 있다.
즉, 아주 작은 시간에 대한 interval인 $h > 0$에 대해, Langevin diffusion은 아래와 같은 역학을 기술할 수 있다.
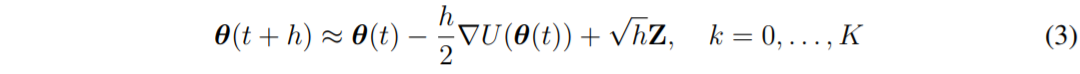
이때, $Z$는 $d$개의 independent standard Gaussian random variable들에 대한 vector이다.
수식 (3)을 정리해보면,
$$ \theta(t + h) - \theta(t) \approx - \frac{h}{2} \nabla U(\theta(t)) + \sqrt{h} Z $$
$$ \frac{\theta(t + h) - \theta(t)}{h} \approx - \frac{1}{2} \nabla U(\theta(t)) + \frac{1}{\sqrt{h}} Z $$
좌변은 미분의 형식을 띄고 있다.
수식 (3)에 기술된 역학은 Langevin diffusion으로부터 sampling하여 근사할 수 있는 간단한 방법으로 적용될 수 있다.
임의의 $K$에 대하여, 전체 time period의 길이인 $T=Kh$에 이와 같은 사실을 적용시기키 위해서는, $\theta_0$를 process의 초기 상태로 설정하고 수식 (3)에서 $h, 2h, ... Kh$ 시점에 대한 process의 값을 포함하도록 반복적으로 sampling하면된다.
$\theta_k = \theta(kh)$라고 표기할 수 있다.
어쨌든 우리는 고정된 시간 $T$에서 Langevin diffusion으로부터 sampling에 대해 관심이 있으니, 더 작은 오일러 상수처럼 h를 매우 작은 값으로 적용하면 된다.
h를 충분히 작게 주었을 때 정확도가 우리가 원하는 정도까지 도달할 수 있다.
하지만, 실전에서 매우 작은 h를 구하는 것은 어려운 일이다.
2.2 Approximate MCMC using the Langevin Diffusion
Langevin Diffusion는 $\pi$라는 고정된 분포를 가지고 있는데, 이것은 stochastic process가 MCMC알고리즘의 기초로써 고려할 수 있다는 것을 자연스럽게 생각할 수 있다.(난 자연스럽지 않지만,,)
사실 Langevin Diffusion의 역학을 정확하게 simulate하는 것이 가능하다면, MCMC 결과를 discrete time-point로 설정하여 사용할 수 있지만, 일반적인 $\pi(\theta)$는 계산 불가능하다.
그러다보니 사람들은 수식 (3)번인 Euler approximation을 사용하여 sampling하는 것에 의존하고 있다.
3) 섹션 3에서는 확률적 경사 MCMC 프레임워크를 랑주뱅 확산을 넘어 특별한 경우로 주어진 많은 인기 있는 확률적 경사 MCMC 알고리즘이 있는 확률적 미분 방정식의 일반 클래스로 확장한다. 많은 MCMC 알고리즘과 마찬가지로 확률적 경사 MCMC는 알고리즘의 효율성에 영향을 미치는 조정 매개 변수를 가지고 있다.
4) 전통적인 MCMC 알고리즘 조정을 위한 표준 진단은 확률적 경사 MCMC에 적합하지 않으며, 섹션 4는 확률적 경사 MCMC 알고리즘의 조정 및 수렴 평가를 위한 메트릭으로 커널 스타인 불일치를 소개한다.
5) 제5절에서는 데이터가 독립적이고 모델 매개변수가 실제 공간에서 연속적인 경우를 넘어 새로운 설정으로 이러한 알고리즘을 확장하는 최근 작업의 일부를 검토한다.
6) 시뮬레이션 연구는 섹션 6에서 제공되며, 속도와 정확성 사이의 균형을 설명하기 위해 몇 가지 확률적 경사 MCMC 알고리즘을 기존 MCMC 방법과 비교한다.
7) 마지막으로, 섹션 7은 논문의 주요 요점에 대한 논의로 마무리되며 향후 연구를 위한 몇 가지 영역을 강조한다.
'개인 공부 정리 > Bayesian' 카테고리의 다른 글
| [논문 소개] On Uncertainty, Tempering, and Data Augmentation inBayesian Classification - 0.Abstract (0) | 2022.12.17 |
|---|---|
| [논문 소개] Cold Posteriors through PAC-Bayes (0) | 2022.11.06 |
| [논문 리뷰] Stochastic gradient Markov chain Monte Carlo - 1.Introduction (0) | 2022.01.15 |
| [논문 소개] Noise Contrastive Priors for Functional Uncertainty (0) | 2022.01.10 |
| [논문 비평] Variational AutoEncoder Bayes (1) | 2021.12.20 |

