| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 파이썬
- 빅데이터
- 강화학습
- 논문리뷰
- uncertainty
- 리눅스
- Graph
- Crawling
- pytorch
- GNN
- 텍스트마이닝
- bayesian
- 데이터분석
- R
- AI
- dropout
- 우분투
- 백준
- selenium
- DATA
- 코딩테스트
- pandas
- 크롤링
- VAE
- PYTHON
- 텍스트분석
- 베이지안
- 알고리즘
- 불확실성
- YarinGal
- Today
- Total
끄적거림
GCN, Graph Convolutional Network 설명 본문
https://www.youtube.com/watch?v=YL1jGgcY78U
https://arxiv.org/pdf/1811.11103.pdf
위의 논문을 알게 되었는데 GCN에 대한 내용을 기본적으로 깔고 들어가기 때문에 GCN을 먼저 공부해보고 해당 논문을 리뷰하도록 하겠다.
GCN은 위의 동영상 강의를 정리해둔 것이니 직접 듣는 것을 추천한다.
1. Graph?
GCN(Graph Convolutional Network)에서 conv는 우리가 CNN을 통해 많이들 알고 있는 개념이고, Network는 Neural Network를 의미하니, Graph에 대해서 이해하면 전체적으로 이해하는데 도움이 될 듯하다.
흔히 CS(Computer Science)에서 graph는 아래와 같이 어떤 관계망을 나타내는 자료구조로 쓰인다.
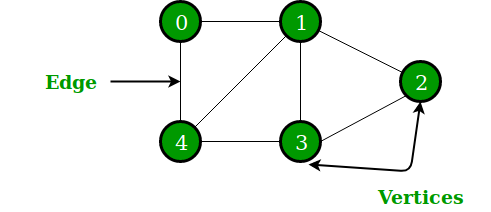
graph는 edge와 vertices로 이루어져 있는데, edge는 link, vertices는 node라고도 불리며, 특히 link는 방향이 있는것과 E없는 것으로 graph의 종류가 나뉜다.
또한, edge도 중요도를 나타내는 것과 연결 여부만 나타내는 것에 따라 두 종류로 나뉜다.
네비게이션에서 각 지역과 도로를 나타내는 자료구조라고 생각하면 편하다.
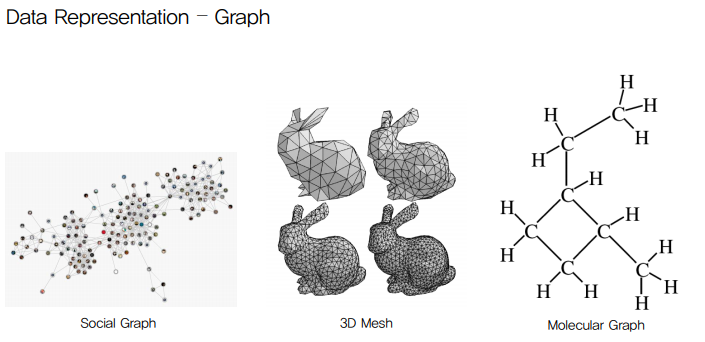
이런 자료구조는 어떻게 활용되냐면, Social 구조, 3D image, 분자 구조 등의 상태를 나타낼 때 사용된다.
1.1 Graph Representation
그러면 이 graph를 어떻게 나타낼 수 있을까?
이 번 시간에는 크게 두 가지로 나타낼 수 있다.
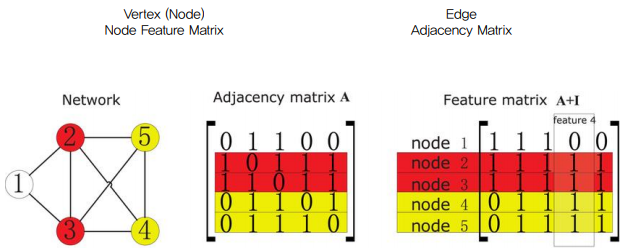
- Adjacency Matrix
- 각 행과 열이 순서대로 노드를 의미하며, 각 노드들이 연결되어 있는지(=두 node 사이에 edge가 있는지 여부)를 정수로 나타낸 행렬로써 표기한다.
- Graph의 종류에 따라 단순 0,1로 element들이 채워지지 않고, 실수가 되기도 한다.
- 위 그림의 예시로 보자면, 1번 node는 2번과 3번 node에 연결이 되어 있으므로, 행렬의 첫 번째 row와 column에 [0, 1, 1, 0, 0]으로 채워진 것이다.
- 행렬의 사이즈는 N by N이 된다.(node가 N개일때)
- Node Feature Matrix
- 각 노드들의 feature를 나타낸 행렬이다.
- 예를 들어 Social 관계망이라고 가정하면, 각 노드는 사람이 될 것이고, 각 사람이 갖고 있는 feature로 성별, 연령 등의 정보가 되겠다.
- 이와 같은 성질로 행은 노드의 수가 되겠지만, feature 수만큼의 열을 가지고 있다.(N by F, N=# of node, F=# of feature)
2. Graph Convolutional Network(GCN)
2.1. Convolution Layer
예를 들어, 32 X 32 X 3의 크기를 갖는 image data가 있다고 해보자.
Convolution Filter(Kernel)라는 것을 이용하여 image를 순회하면서 dot product를 계산하고, 기존의 데이터로부터 filter를 이용하여 새로운 tensor(=activation map)를 만드는 것을 convolution 이라고 한다.
이러한 연산에서 filter의 깊이(depth)를 receptive field라고 하는데, 이 receptive field가 깊을수록 더 깊은 계산 layer가 나오게 되고, NN의 깊은 곳에서는 더 깊은 receptive field가 발생하고, 얕은 곳에서는 얕은 receptive field가 발생한다.
이 conv 연산의 특징 중에 하나는 바로 weight sharing이다.
이미지 task에서 MLP를 이용한 방법론은 모든 노드와 layer가 이어져 있기 때문에(fully-connected) parameter의 수가 기하급수적으로 늘어났고, 또한 image에서 pixel이 조금이라도 틀어지면 기존의 parameter가 변질되기 때문에 성능이 안좋아지는 단점이 있다.
하지만 CNN에서는 filter가 image를 순회하며 연산하기 때문에 parameter를 공유할 수 있게 된다.
참고글(https://techblog-history-younghunjo1.tistory.com/125)
이런 특성을 weight sharing이라고 부르며 이로 인해 학습할 paramter 수가 적어지며, overfitting의 문제점도 해결할 수 있다.
또한, conv filter를 사용하다보니 local한 feature를 잘 뽑아낼 수 있다는 장점과 down-sampling에 대한 효과를 얻을 수 있다는 장점이 있다.
이런 conv filter를 사용하면 image로부터 어떤 feature들을 뽑아내고 activation map이 업데이트가 되면서 연산이 진행되는데, 이러한 과정을 GCN에서도 동일하게 적용하고자 한다.
2.2. Update GCN
핵심은 이것이다.
앞서 1.1에서 보았던 node feature matrix를 update하여 어떤 task를 수행하는 것이다.
각 node들이 갖는 feature이 update되는 것이 목표라면, 앞서 2.1에서 보았던 conv layer를 이용하여 feature update를 수행하는 것이다.
conv layer는 local한 부분의 feature들을 모아서 연산했다면, 이와 동일한 방식으로 graph도 주변에 있는 부분들로 update를 하자는 것이다.
위 그림의 수식에서 W는 weight를 의미하고, l은 l번째 Layer, H는 Hidden state(=각 layer를 거치고 난 뒤의 node feature matrix)라는 뜻이다.
즉, 하늘색으로 표기된 항을 풀어서 설명하면, node 1의 l번째 node feature matrix에 l번째 weight를 행렬곱한 것이라고 보면 된다.
따라서, 위의 수식이 의미하는 것은 node1의 l+1번째 node feature matrix를 나타낸 것인데, 이는 node 1과 인접한 모든 node들의 node feature matrix에 각 weight를 곱하고 bias를 더하여 activation function을 씌워주어 업데이트하는 과정이다.
또한, 모든 node의 weight가 다 동일하기 때문에 weight sharing을 가능하게 했다.
따라서, 이 업데이트되는 과정은 convolution 연산과 같이 local한 정보를 이용하고, weight sharing을 한다는 특징을 가지기 때문에 GCN이라고 부르는 것이다.
여기에, 각 node들을 업데이트하려면 해당 node의 인접한 node들의 정보, 또 그 node의 인접한 node의 정보, .... 이런식으로 연쇄적으로 연결되어 있기 때문에, 이러한 connectivity의 정보를 갖고 있는 Adjacency Matrix를 이용하여 구할 수 있다.
각 node의 n번째 인접한(hop) node의 연결 여부를 알기 위해서는 간단하게 Adjacency Matrix를 n번 곱하면 된다.
그러면 간단한 행렬 연산으로 convolution 연산을 수행할 수 있게 된다.
2.3. Readout
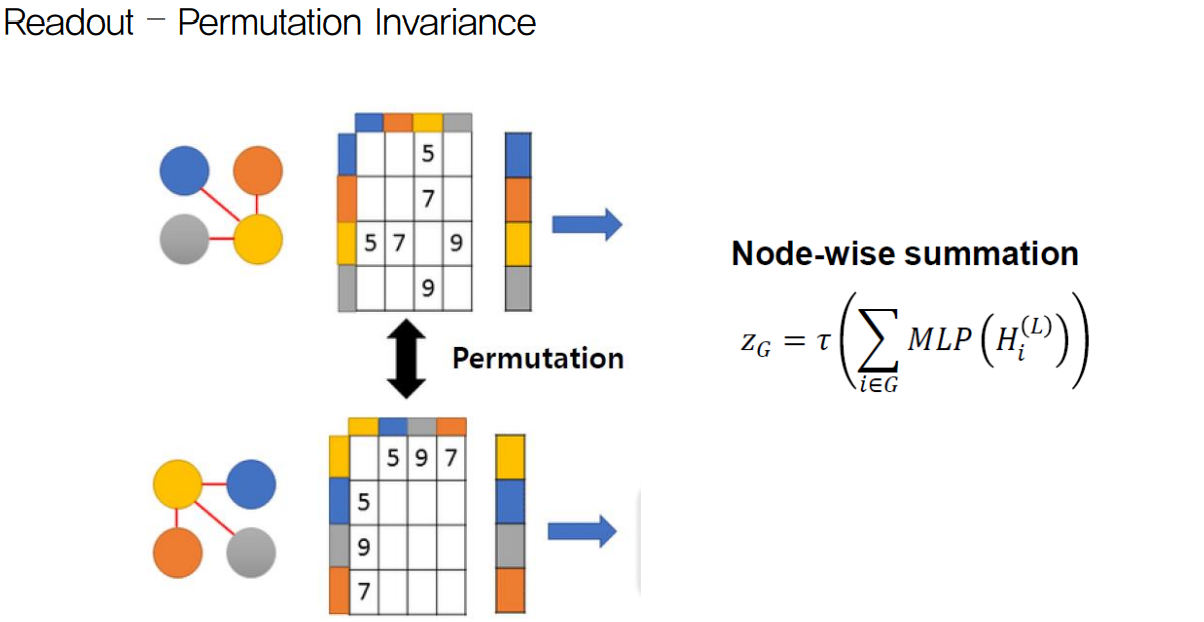
하지만 여기에 한 가지 함정이 있다.
위 그림처럼 같은 graph 구조를 갖지만 위치가 달라짐으로 인해 Adjacency Matrix가 달라지게 되는 것이다.
이러한 오류를 방지하기 위한 방법이 Readout이다.
다른말로는 Permutation Invariance라고도 하는데 Permutation은 graph structure를 의미하고 invariance는 관계없이라는 뜻이므로, graph sturcture가 어떠하든 상관 없이 같은 위상을 갖는 graph라면 같은 결과를 내야한다는 의미이다.
그에 대한 방법은 그림의 오른쪽 수식과 같다.
2.2에서 보았던 것처럼 l번째 node feature matrix에 대해 MLP(=fully connected)를 씌워주어 sum을 한 후 activation을 씌우면 같은 위상에 대해서 다른 node 위치를 갖는 graph에 대해 동일한 결과를 낼 수 있다는 것이 수학적으로 증명되었다고 한다.
이 Readout 방법이 가장 간단하면서도 효율적인 방법이라고 하니 기억해두자.
2.4. Overall Structure of GCN
이제 GCN의 전체적인 구조에 대해 살펴보자.
위 그림과 같이, Node Feature Matrix인 X와 Adjacency Matrix인 A를 갖는 graph를 input으로 하였을 때, 원하는만큼의 convolution 연산을 거치고(중간중간에 activation function이 있긴하다.), Readout을 적용한 후 fully connected layer를 거친 후 우리가 원하는 결과를 얻게된다.
그렇게 나온 output과 실제 true label 혹은 true value와의 loss를 구하고 그 loss를 minimize하게끔 weight들을 업데이트 하게끔 학습이 이루어질텐데, Readout과 fully-connected layer는 우리가 흔히 아는 weight이기 때문에 설명은 넘어가고. convolution layer에서는 각 node들의 node feature들에 대한 weight를 업데이트하게 된다.
여기까지가 GCN에 대한 기본적인 개념을 설명한 것이고 이후부터는 GCN을 활용한 advanced model이 나온다.
3. Advanced Techniques of GCN
3.1. Inception
왼쪽에 보이는 그림이 일반적인 inception 모듈이다.
하나의 filter만 적용시키는 것이 아니라 여러 size의 filter들을 병렬로 적용한 후에 concat시키서 다음 layer를 만드는 모듈이다.
좋은 발상이고 기존의 conv layer보다 좋은 성능향상을 가져왔지만, depth가 깊어지는 단점이 있고 이를 해결하기 위해 오른쪽 그림처럼 1 by 1 filter를 적용시켜서 computation efficiency를 향상시키는 방법도 등장하였다.
그러면 inception 모듈을 GCN에 어떻게 적용시킬 수 있을까?
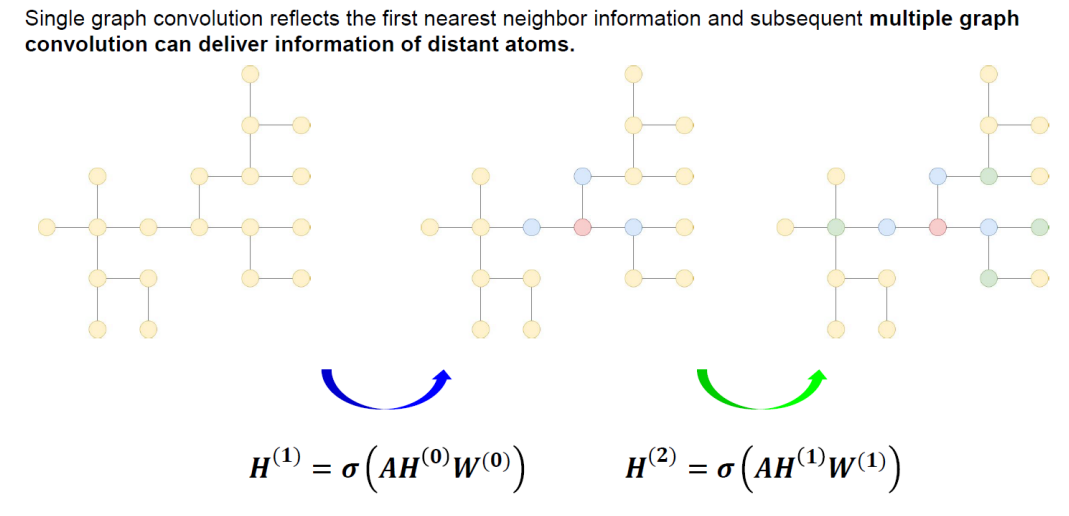
결국 inception 모듈은 다양한 크기의 filter를 사용하자는 것이 핵심이었고, 이를 GCN에 적용시키면 다양한 hop의 인접한 node들의 feature를 사용하는 것으로 적용시킬 수 있다.
그러면 이 다양한 hop은 어떻게 만들 수 있을까? 바로 Adjacency Matrix를 그만큼 곱해주면 된다.
이에 해당하는 GCN의 구조가 아래의 그림이다.
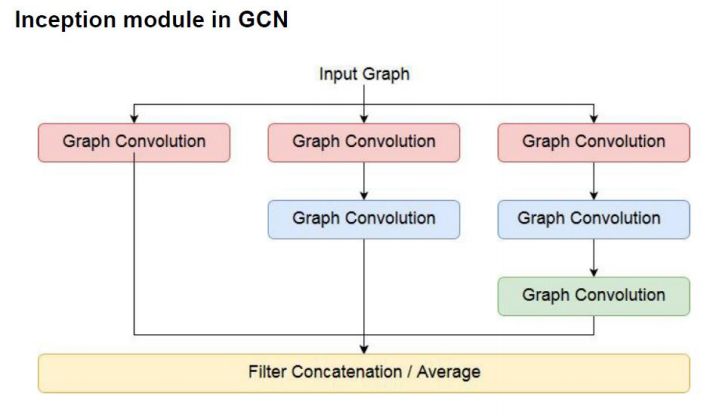
3.2. Skip Connection
ResNet에서 사용되었던 Skip conncetion이다.
NN의 depth가 깊어질수록 성능이 오히려 감소하는 현상이 발생했었는데, 이를 skip할 수 있는 모듈을 만들어주어 성능이 오로지 우상향 할 수 있게끔 해주었다.
이를 GCN에 동일하게 적용하면, 위 그림의 왼쪽처럼 볼 수 있다.
오른쪽은 skip을 진행할 때 trick을 적용시킨 것인데, 기존에 skip connection은 skip term과 conv layer term을 동일한 가중치를 두어 합하였다면, 오른쪽은 두 항에 대해 다른 가중치를 두어 합치게 하는 trick을 적용한 것이다.
3.3. Attention
Attention은 "Attention is all you need"라는 논문에서 처음 등장한 개념으로 엄밀히 말하면 CNN은 아니지만 개념을 간단히 짚고 넘어가자면,
기존의 GCN은 자기 자신 node를 포함하여 인접한 node의 feature를 합하여 업데이트를 진행하는데, 이 때 각 인접한 node의 feature를 동일한 가중치로 여기고 합하게 된다.
이 점을 개선하여, 동일한 가중치를 주지말고, 특정 비율로 합하여 업데이트를 하자는 것이 attention을 이용한 GCN의 목표이다.
이때 어느정도의 가중치를 줄것인지를 결정하는 것은 각 노드끼리의 correlation으로 정하게 된다.
상관성이 높을수록 그만큼 더 높은 weight를 주어 합하게 된다.
