| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 강화학습
- 빅데이터
- 백준
- 불확실성
- PYTHON
- pandas
- selenium
- VAE
- 리눅스
- 알고리즘
- GNN
- 데이터분석
- Graph
- 파이썬
- bayesian
- 크롤링
- 논문리뷰
- YarinGal
- R
- DATA
- Crawling
- uncertainty
- pytorch
- 텍스트분석
- 텍스트마이닝
- dropout
- 코딩테스트
- 베이지안
- 우분투
- AI
- Today
- Total
끄적거림
[논문 리뷰] Bayesian Graph Convolutional Neural Networks for Semi-Supervised Classification - 0.Abstract ~ 3.Background 본문
[논문 리뷰] Bayesian Graph Convolutional Neural Networks for Semi-Supervised Classification - 0.Abstract ~ 3.Background
Signing 2021. 8. 18. 22:12최근 Graph Neural Network 부분이 트렌드가 되면서 Bayesian과 결합한 모델들도 연구되고 있어서 한 번 공부해보고자 한다.
논문: https://github.com/huawei-noah/BGCN
GitHub - huawei-noah/BGCN: A Tensorflow implementation of "Bayesian Graph Convolutional Neural Networks" (AAAI 2019).
A Tensorflow implementation of "Bayesian Graph Convolutional Neural Networks" (AAAI 2019). - GitHub - huawei-noah/BGCN: A Tensorflow implementation of "Bayesian Graph Convolutional N...
github.com

2019년 AAAI에 올라온 논문이며, 베이지안을 결합한 괜찮은 논문이라 생각되어 리뷰해보겠다.
Abstract
Recently, techniques for applying convolutional neural networks to graph-structured data have emerged. Graph convolutional neural networks (GCNNs) have been used to address node and graph classification and matrix completion. Although the performance has been impressive, the current implementations have limited capability to incorporate uncertainty in the graph structure. Almost all GCNNs process a graph as though it is a ground-truth depiction of the relationship between nodes, but often the graphs employed in applications are themselves derived from noisy data or modelling assumptions. Spurious edges may be included; other edges may be missing between nodes that have very strong relationships. In this paper we adopt a Bayesian approach, viewing the observed graph as a realization from a parametric family of random graphs. We then target inference of the joint posterior of the random graph parameters and the node (or graph) labels. We present the Bayesian GCNN framework and develop an iterative learning procedure for the case of assortative mixed-membership stochastic block models. We present the results of experiments that demonstrate that the Bayesian formulation can provide better performance when there are very few labels available during the training process.
물론 그동안의 GCN으로도 충분히 좋은 성능을 냈지만, uncertainty를 구하지는 못하였고, 또한 Bayesian approach를 이용하여 더 좋은 성능을 내었다고 한다.
또한 중요한 부분만 찝어서 보면, 모수적인 분포들을 사용하여 random graph를 만들었고, assortative mixed-membership stochastic block model이라는 것을 사용하였다고 한다.
1. Introduction
1) 최근에 GCN에 대해 많은 연구와 시도들이 있었고, 또 많은 발전들이 이루었었다.
2) 본 논문은 지난 과거의 연구들과 비교했을 때, 베이지안 프레임워크를 사용하였고, 모수적 분포를 사용한 random graph를 사용하였다.
3) joint inference를 하기 위해 adjacency matrix와 feature matrix, label matrix를 결합하여 사용하였다.
4) 최종적으로, 계산복잡도가 다소 걸리는 단점이 있지만, 아래와 같은 장점들을 contribution으로 꼽았다.
- 더 적은 데이터로 학습 가능
- uncertainty를 구하는데 더 좋은 성능을 냄
- noise나 adveersarial attack으로부터 robustness를 더 잘 보임.
5) 이 논문에서 BGCN(Bayesian Graph Convolutional Network)을 보여주고 어떻게 inference했는지를 보여줌.
6) semi-supervised node classification과 graph의 위상의 randomness로부터 아키텍쳐가 잘 복원되는지도 실험함.
2. Related Work
1) 주로 본 절에서는 GCNN(Graph Convolutional Neural Network), GAT(Graph Attention Network), Bayesian Approach에 대한 역사와 흐름을 소개하고 있다.
2) 거의 주요 논문 소개와 다름 없으므로 논문상에서 확인하면 되겠다.
3. Background
GCNN, Graph Convolutional Neural Network
1) 주로 node의 label을 identify하는데 GCNN을 사용
2) 표시
 |
Observed Graph |
 |
set of nodes |
 |
set of edges |
 |
measure data or deerive feature |
 |
1) label in classification 2) real-value in regression |
 |
subset of the nodes |
 |
measure labels |
 |
weight of the neural network at layer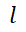 |
 |
output feature from layer |
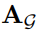 |
output feature가 각 layer에서 얼마나 mixed accross되었는지를 나타내는 matrix |
 |
final output for an L-layer network |
3) weight와 mixed accross matrix를 곱하고, non-linearity function을 씌우는 과정으로 layer를 학습시켜감.

4) weight를 학습하는 것은 실제 label과 예측치의 차이를 최소로 하게끔 만들면서 weight를 학습
5) 성능을 향상시키는 것은 아키텍쳐에 따라 향상됨.(CNN, attention, skip-connection & gate를 적용시키는 GNN)
6) node들 사이의 관계를 나타내는 ground-truth를 구하는 것이 목적인데, 이때, noisy data를 사용하거나 model assumption을 사용하기도 하는데 사실 이런 것들은 성능에 안좋은 영향을 끼친다.
7) 만약 잘못된 edge가 있다면, 학습하는데 잘못 학습하여 다른 강한 관계를 갖는 node의 edge를 놓칠 수 있기 때문이다.
8) 그래서 attention을 사용하기도 하는데 이것의 장점은
- 몇몇 edge들이 의미있는 관계를 나타내는 것이 아님을 학습할 수 있다.
- node가 다른 node에게 주는 영향을 줄일 수 있다.
9) 하지만 단점도 있는데
- 계산복잡도가 높고,
- 반드시 있어야할 edge를 제대로 학습하지 못하기도 하며,
- 앙상블 모델에서도 한계를 보인다.
10) 참고 : 2021.08.15 - [개인 공부 정리/Bayesian] - GCN, Graph Convolutional Network 설명
GCN, Graph Convolutional Network 설명
https://www.youtube.com/watch?v=YL1jGgcY78U https://arxiv.org/pdf/1811.11103.pdf 위의 논문을 알게 되었는데 GCN에 대한 내용을 기본적으로 깔고 들어가기 때문에 GCN을 먼저 공부해보고 해당 논문을 리뷰하..
signing.tistory.com
BNN, Bayesian Neural Network
1) 주어진 input X, 그에 따른 output Y가 있으면, 그 관계를 나타내는 function(layer의 수라던가, 어떤 activation을 사용할지 등)을 찾는 것이 우리의 목표다.
2) 우리는 이 function의 구성이 weight에 달려 있음을 알고 있는데, bayesian 관점에서는 이 weight들이 random variable(R.V.)인 것이다.
3) 논문에서는 weight(W)가 R.V.라고 하면 output도 R.V.라고 하는데 이 말이 맞는 말인지는 의심이 된다.
왜냐하면, 주어진 데이터 X,Y가 있을 때, W가 R.V.로써 작용하는 것이 bayesian인데 W가 not deterministic하면, output도 R.V.라는 이야기는 틀렸다고 생각한다.
이에 대해 의견을 주시면 감사하겠다.
4) 어쨌거나, 이러한 R.V.인 W의 확률분포를 posterior(사후확률)라고 한다. 그에 대한 식은 아래와 같다.

5)

왼쪽에 보이는 수식을 우리는 likelihood라고 볼 수 있다.
likelihood는 그냥 확률이다.
자세한 설명은 [논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 2.Related Work(2) 에 나와있으니 참고하시길..
6) 그런데 문제는 (3)번 식이 계산할 수 없는 식이라는 것이다.
7) 이러한 문제를 해결하기 위한 많은 노력들이 있어왔다.
- expectation propagation
- variational inference
- Markov Chanin Monte Carlo method
8) 특히, (3)번 식을 MC-dropout으로 해결한 아주 깔끔한 방법도 있다.

자세한 설명은 아래 포스팅을 확인바란다.
[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 1.Prologue
[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 1.Prologue
[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 1.Prologue [논문 리뷰] Dropout as a Bayesian Approximation 설명 - 2.Abstract [논문 리뷰] Dropout as a Bayesian Approximation 설명 - 3.Introduce..
signing.tistory.com
'개인 공부 정리 > Bayesian' 카테고리의 다른 글
| [자료 정리] VAE 읽을거리 및 실습들 (0) | 2021.08.28 |
|---|---|
| [논문 리뷰] Bayesian Graph Convolutional Neural Networks for Semi-Supervised Classification - 4.Methodology (0) | 2021.08.21 |
| GCN, Graph Convolutional Network 설명 (1) | 2021.08.15 |
| Entropy as Uncertainty Measure (0) | 2021.08.07 |
| Mixture Density Network 정리 (0) | 2021.08.04 |

