| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- AI
- 텍스트마이닝
- DATA
- uncertainty
- pandas
- bayesian
- YarinGal
- Crawling
- pytorch
- GNN
- 크롤링
- Graph
- 빅데이터
- 백준
- 불확실성
- 코딩테스트
- selenium
- 베이지안
- 논문리뷰
- 강화학습
- 우분투
- 데이터분석
- R
- dropout
- VAE
- 리눅스
- 알고리즘
- 텍스트분석
- 파이썬
- PYTHON
- Today
- Total
끄적거림
[논문 리뷰] Disentangling the Roles of Curation, Data-Augmentation and the Prior in the Cold Posterior Effect 본문
[논문 리뷰] Disentangling the Roles of Curation, Data-Augmentation and the Prior in the Cold Posterior Effect
Signing 2021. 10. 24. 21:16[논문 소개] Cold Posterior Effect 관련 논문들
[논문 소개] Cold Posterior Effect 관련 논문들
베이지안 관련 최신 논문들을 찾다보니 또 하나의 새로운 개념을 알게 되었다. Cold Posterior Effect(이하 CPE.)라는 개념인데 아직 계속해서 공부중이고, 이 것을 파다보니 연관된 다른 논문들이 많이
signing.tistory.com
cold posterior를 연구 타겟으로 정했고, 공부하다보니 cold posterior가 data-aug.에 좋다는 논문을 여럿 보았다.
그 중에서 핵심적으로 다루는 논문인 것 같아 리뷰해보고자 한다.
abstract 같은 부분은 위의 이전의 포스팅에 해석해 두었으니 바로 본론으로 들어가겠다.
1. Introduction
1.1
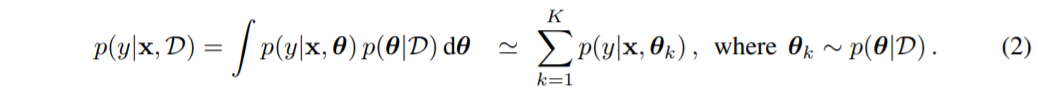
posterior predictive로 task 수행할 수 만 적분 때문에 계산이 불가능하다.
그래서 MC sampling을 이용하여 근사하였다.
1.2
MCMC방법론이 implement하기 쉽지만, 대용량의 dataset이거나 모델이 큰 경우, SG-MCMC를 사용한다.
1.3
베이지안 딥러닝은 accuracy와 효율적인 approxiamtion측면에서 좋은 연구를 거두고 있다.
최근 연구에 따르면 Cold Posterior Effect(이하 C.P.E.)는 predictive 성능향상을 가져왔다.
C.P.E.는 기존의 베이지안 패러다임에서 벗어나지만, heuristic하게 실용적이다.
1.4
CPE는 실제 적용과 이론에 대해 문제가 있다.
많은 연구자들이 이 현상을 설명하기 위해 가설을 제안하고 있다.
그에 대한 내용은 다음과 같다.
- Isotropic Gaussian Prior
- likelihood model
- inaccurate inference
- data augmentation
하지만 이런 연구에도 불구하고 C.P.E.에 대해 직감적으로 와닿지 않는다.
1.5
위 문제들에 대해 본 논문에서는 다음과 같은 contribution을 갖는다.
- Dataset curation hypothesis : C.P.E.는 실제 curation dataset에서 발생되지 않지만, curation정도가 다양하게 통제된 실험에서 생성될 수 있음을 경험적으로 보여준다.
- Data augmentation hypothesis : data augmentation은 필요하지만, C.P.E.가 존재하기 위해서는 필요하지 않다는 것을 경험적으로 보였다.
- Bad prior hypothesis : C.P.E.와 prior가 강하게 연결된 것과 prior와 likelihood의 중요성을 평가하는 실험을 했다
1.6
C.P.E.가 synthetic curation, data augmentation, bad-prior와 얼마다 다른 이야기인지 설명하는 논문이다.
C.P.E.를 3가지 factor로 재해석했다.
2. Cold Posteriors: Background & Related Work
2.1
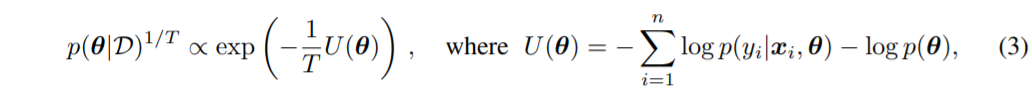
기존 posterior에서 potential energy function인 U(theta)에 1/T만큼의 scaling(=tempering했다고도 표현)을 적용한 형태이다.
2.2
T=1이면 그냥 Bayes Posterior가 되고, T->0이면 MAP estimation에 posterior를 inference하는 것이다.
2.3
Note that, besides tempering the posterior as in Equation 3, one can also temper only the likelihood resp. scale only the log-likelihood, as is commonly done in VB, see Section 2.3 in (Wenzel et al., 2020). It is worth pointing out though that both variants are practically equivalent if the prior variance is multiplicative in log-prior pre-factors (such as for Gaussian priors) and if sufficiently many prior variances are grid-searched over as part of the inference pipeline, such that for the best performing posterior-tempered model there is a corresponding likelihood-tempered model with variance scaled by 1/T in the grid and vice versa.
해석 못함..ㅠ
2.4
C.P.E.가 잘못 산출될 수 있는 3가지 주요 요소가 있다.
- model misspecification : likelihood 모델이 잘못되었을 경우
- bad priors : prior가 BNN에서 불충분하게 사용되었을 경우
- inaccurate inference : posteior에 대한 부정확한 inference가 되었을 경우
2.4.1 Inaccurate Inference Hypothesis
C.P.E.가 SG-MCMC로 true posterior approximation을 잘 할 수 있었지만, 실제로 계산할 수 없는 true posterior에 접근할 수 없는데 근사했다는 문제가 있다.
How Good is the Bayes Posterior in Deep Neural Networks Really?에서 제안한 방법을 보면 ensemble statistics와 비교를 했는데, 이것이 inference 메커니즘에 문제가 있다.
여러 실험을 하면서 모니터링을 해봤지만 우리가 하는 inference가 정확한 것인지는 확신할 수 없었다.
Why Cold Posteriors? On the Suboptimal Generalization of Optimal Bayes Estimates 라는 논문에서 full-batch Hamiltonian Monte Carlo(이하 HMC)로 하는 inference가 좋았고, data augmentation을 하지 않을 때는 C.P.E.가 사라졌다고 한다.
이러한 결과가 C.P.E.에서 inference가 잘못되었다는 증거로 오인할 수 있지만, 그렇지 않다고 생각할 근거가 있다.
data augmentation을 하지 않았을 때 How Good is the Bayes Posterior in Deep Neural Networks Really?에서 나와있는 모델에 적용된 SG-MCMC 기반 inference를 통해 C.P.E.가 발생하지 않음을 확인했다고 한다.
이를 통해 SG-MCMC inference가 특정 설ㅈ어에서 정확하거나, C.P.E.가 나타나기 위해 부정확한 inference가 필요하지 않다는 결론을 낼 수 있다.
2.4.3 Data Augmentation Hypothesis(model misspecification)
C.P.E.는 data augmentation에 좋은 수단 중 하나라고 한다.
이 주장은 ResNet CIFAR10 설정에서 data augmentation을 안하는 것이 C.P.E.를 제거하는데 충분하다고 하는 주자을 근거로 한다.

