[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 4.Related Research (3): Background(Bayesian Neural Network, Variational Inference, Re-parameterization trick)

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 1.Prologue

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 2.Abstract

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 3.Introduce

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 4.Related Research (1): Background(MC-Integration, Dropout)

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 4.Related Research (2): Background(Gaussian Process)

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 4.Related Research (3): Background(Bayesian Neural Network, Variational Inference, Re-parameterization trick)

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 5.Methodolgy

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 6.Experiment

[논문 리뷰] Dropout as a Bayesian Approximation 설명 - 7.Conclusion

[논문 실습] Dropout as a Bayesian Approximation 실습 코드 - pytorch ver

---

 

Bayesian Neural Network(이하 BNN)

이번 시간엔 BNN에 대해서 알아볼 예정인데, 그 전에 한 가지 질문을 던지겠다.

데이터가 주어졌을 때, 이 데이터와 가장 likely한(유사한) function을 어떻게 정의할 수 있을까?

대답은 "베이지안 관점으로 볼 때, 함수의 공간에서 prior을 넣으면 된다."

쉽게 말해서 함수 f에 확률을 부여하겠다는 의미이다.

다음의 그림을 보면 보다 이해가 수월할 것이다.

출처: Weight Uncertainty in Neural Networks

single layer Neural Network를 생각해보겠다. 이것도 엄연히 하나의 함수다.

왼쪽 그림이 우리가 흔히 알고있는 NN 모델이다.

각 노드들을 잇는 weight들이 하나의 모수로 존재하는 deterministic한 model이다.

반면 오른쪽은 weight들이 하나의 모수로 존재하는 것이 아닌 어떤 분포로써 존재한다.

지난 시간 G.P.R의 kernel에 대해서 이야기할 때도 이 이야기가 나왔다.

그렇다.

G.P.R은 Bayesian이다.

반면, 엄밀히 말해서 G.P.는 Bayesian이 아니다.

 

그럼 다시 돌아와서, 함수공간에 prior를 준다는 말은 함수 f에 확률 및 분포를 부여하겠다는 의미라고 했다.

이 확률(=분포)만 알면 우리는 함수가 어떻게 존재하는지 그 특성에 대해서 수월하게 이해할 수 있을 것이다.

그리하여 p(f)에 대해서 정의할 수 있다고 가정해보자.

그런 다음, 그 정의된 함수 f와 주어진 input인 X가 주어졌을때의 Y의 분포 또한 계산할 수 있을 것이다.

그러면 bayes rule에 의하여 우리는 data가 주어졌을 때의 함수 확률 p(f|X,Y)를 구할 수 있다.

여기서 bayes rule이라하면 무엇인고,,?

 

Bayes rule

출처: wiki

감사하게도 위키피디아에 잘 나와있다.

출처: ko.wikipedia.org/wiki/%EB%B2%A0%EC%9D%B4%EC%A6%88_%EC%A0%95%EB%A6%AC

베이즈 정리 - 위키백과, 우리 모두의 백과사전

 

그럼 다시 위의 식을 이렇게 바꿀 수 있다.

f를 W로 바꾸었다.

사실 함수는 weight parameter만 알고 있으면 그것이 곧 함수이기 때문이다.

각 항들이 의미하는 바를 posterior, likelihood, prior로 표현할 수 있다.

이 것은 위에 링크 걸어둔 위키피디아에 잘 설명이 되어있으니 한 번 읽어보길 바라고, 나는 지금부터 이 단어들을 자주 사용할 것이다.

 

좋다!

그래서 이제 우리는 결국 posterior까지 구할 수 있다.

그 다음 이 posterior로 Marginalization이라는 것을 할 수 있다.

Marginalize

여기서 theta는 weight라고 볼 수 있다.

결국, theta에 대한 prior와 theta가 주어졌을 때의 data에 대한 수식으로 data에 대한 prior를 구할 수 있다.

이것이 posterior와 어떤 관련이 있냐면,

New data distribution with Marginalization

위의 수식처럼 새로운 data인 x*, y*가 주어졌을 때의 분포를 구할 수 있게된다.

이 뜻은 marginalize로 새로운 데이터에 대한 예측이나 분류가 가능해진다는 의미이다.

 

아쉽게도 위의 수식은 실제로 계산하는데 많은 리소스가 요구된다.

실질적으로 계산을 할 수 없는 수준이다.

이를 해결하는 문제는 나중에 포스팅될 예정이다.

 

 

 

Variational Inference(이하 V.I.)

이번 논문에서 가장 중요한 개념 중 하나이다.

이 V.I.는 본 논문 뿐 아니라 지금까지도 연구가 활발히 진행되는 파트이다.

V.I.에서 variational이라는 것은 무엇일까?

variation은 흔히 말해 분산? 분포? 등과 같은 느낌으로 이해하고 있으면 된다.

이런 분포를 inference, 즉, 근사 혹은 추론하겠다는 것이다.

그러면 뭐에 대한 분포의 추론일까?

바로 위에서 살펴보았던 posterior에 대한 추론인 것이다

 

1. posterior를 어떻게 찾을것인가?

posterior는 위에서 p(w|X,Y)로 표현하였다.

그렇다면 posterior를 구하려면 어떻게 해야할까?가 문제가 된다.

위에서는 likelihood와 prior를 곱하면 posterior가 된다고 했다.

가능한 이야기처럼 보이지만 사실 가능하지 않다.

일단 prior를 구하기도 힘들뿐 아니라 그를 이용한 likelihood를 구해야하는데 계산할 수 없는것(intractable)이다.

그래서 나온 해결법이 posterior와 비슷한 분포를 갖는 q라는 분포를 정의하여 둘을 근사시키는 방법이다.

 

2. qθW

여기서 q는 posterior와 비슷한 분포를 갖는 분포라고 생각하면 된다.

임의로 정한 분포인 것이다.

이런 분포를 우리는 variational distribution이라고 한다.

그러면 posterior와 비슷한 이 q라는 variational 분포는 posterior와 어떻게 근사시킬수 있을까?

 

3. Minimize KL Divergence(이하 KL-d)

바로 posterior와 q의 KL-d를 최소화하면 된다.

여기서 KL-d는 어떤 두 분포의 차이라고 생각하면 된다.

이 개념에 대해서는 나중에 따로 포스팅을 하도록 하겠다.

자 그럼 다시 돌아와서, posterior와 q의 KL-d를 최소화한다고 했다.

그러면 두 분포의 차이가 거의 없어지면서 q가 posterior로 점점 근사하게 되어서 이 variational distribution을 posterior대신 사용할 수 있게 된다.

그러나 이 두 분포 사이의 KL-d를 구할 수 있을까?

그럴 수 없다.

왜냐하면 posterior도 모르는데 KL-d는 당연히 구할 수 없기 때문이다.

그러면 생각의 전환이 필요한 시점이다.

 

4. Maximize Evidence Lower Bound(이하 ELBO)

ELBO는 어디서 튀어나왔는고?

ELBO를 알기 위해서는 먼저 데이터의 marginal likelihood를 알아야한다.

기호로는 아래와 같다.

여기서 data의 likelihood는 그렇다 치는데, beta는 measurement noise이고, A는 hyper-parameter라고 보면 된다.

measurement noise란 data를 관측할 때의 noise라고 생각하면 되는데, regression에서 잔차가 normal distribution을 따른다고 가정하는 것과 같은 느낌으로 받아들이면 된다.

최성중 박사님의 edwith 강의 노트에 대한 내 필기

 

일단 수식이 나와서 기분이 다들 안좋아졌을것이라 생각한다.

하지만 자세히 천천히 따라가다보면 그렇게 이해하기 어려운 수식은 아니니 살펴보자.

 

일단은 우리가 잘은 모르지만, data에 대한 marginal log-likelihood가 있다.

각 line by line으로 살펴보자.

1. 이 marginal log-likelihood에다가 간단한 수학적 트릭을 적용시킬 것이다.
   첫 줄을 보면, p(D) 옆에 q(w|theta)가 붙어 있는데 이 전체가 적분으로 둘러쌓여있다.
   하지만, marginal log-likelihood를 상수취급하면 나머지는 어떤 분포에 대한 적분으로 볼 수 있다.
   모든 구간에 대해 어떤 분포의 적분은 1이다.
   그러므로 사실상 data에 대한 marginal log-likelihood에 1을 곱한 것이나 다름 없다.
2. 이제 marginal log-likelihood의 분모/분자에 각각 p(w|D)라는 w에 대한 posterior를 곱해준다.
3. 그렇게 되면 분자에서 marginal likelihood와 posterior가 곱한 꼴이 되므로 조건부 확률 정의에 의해서 p(w, D)의 꼴로 바꿀 수 있다.
4. 이는 다시 조건부 확률 정의에 의해서 p(D|w)*p(w)로 변환이 되고
5. log부분에 분모와 분자에 q(w|theta)를 곱해준 후
6. 적절히 분자, 분모를 이동하여 log의 성질로 분리해주면
7. 결국, marginal log-likelihood는 KL-d와 F[q](=ELBO)의 합으로 볼 수 있다.

이것을 그림을 보면 아래와 같다.

Christopher M.Bishop, Ensemble Learning in Bayesian Neural Networks

또한, ELBO를 구하는 다른 방법은 아래와 같다.

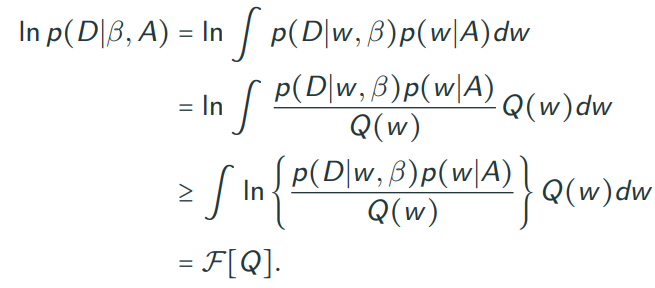
이것은 marginal log-likelihood에서 ELBO가 존재한다는 것을 밝히는 과정이다.

중간의 부등호는 단순히 log를 안으로 넣었을 때, 나타나는 현상이다.

이를 Jensen's inequality라고 하는데 자세한 사항은 wiki를 찾아보면 나오긴한다.

(참고: en.wikipedia.org/wiki/Jensen%27s_inequality)

이렇게 나온 ELBO는 아래와 같이 쓰여질 수 있고, ELBO의 다른 이름은 Variational Free Energe라고도 불린다.

 

그럼 다시 정리해보자.

처음 w에 대한 posterior을 찾는 문제를 variational distribution인 q(w)를 구하는 문제로 바꾸었고 이를 다시 KL-d를 minimize하는 문제로 바꾸었다.

그러나 이 문제가 intractable한 이유로, 이와 동치인 ELBO를 maximize하는 문제로 바꿀 수 있었다.

이러한 일련의 시퀀스를 Variational Inference라고 부른다.

결국 variational distribution을 근사시켜 구하는 것이 V.I.라고 불리는 것이다.

 

 

 

 

 

 

Re-parameterization trick

re-parameterization trick은 Variational Auto-Encoder(이하 VAE)에서 사용된 개념이다.

arxiv.org/pdf/1312.6114.pdf

 

VAE는 위 그림과 같이 input data인 x를 어떤 구조 안에 넣었을 때, 이를 압축시키는 feature 혹은 variable인 z를 지나 다시 원래의 x로 복원되는 과정을 의미한다.

이 논문도 꽤 오래된 논문이지만 한 번 읽어볼 법 하다.

이제 여기서 나온 re-parameterization trick을 살펴보자.

그림에서 보이듯 각 노드들이 있고, backpropagation이 위에서 아래로 흐르게 하고 싶은 것이다.

그러나 논문에 따르면 중간의 z variable이 분포를 갖으면서 확률로써 존재하게 된다.

역전파를 흐르게 하려고 하는데 확률(randomness)이 부여된 분포를 그냥 지나갈 수는 없다.

결국 randomness가 있을 때는 역전파를 계산할 수 없다는 것이다.

re-parameterization trick의 개념은 간단하다.

이 역전파를 흐르게 하기 위해서 randomness가 부여된 stochastic node를 randomness가 존재하는 stochastic 파트와 deterministic 파트로 나누는 것이다.

그렇게 되면 deterministic 파트로 역전파가 흘러 역전파를 계산할 수 있게 되는 것이고, 그렇다 하더라도 randomness를 버리는 것이 아닌 여전히 유지하고 있는 것이다.

물론 이 randomness가 그 전보다는 다소 부정확하고 작아질 수가 있다.

 

---

 

 

 

여기까지가 본 논문을 이해하기 위해서 사전에 알아야할 background이다.

너무 간단간단히 설명한 것 같아 마음에 걸리지만,

이정도만 알아도 논문을 이해하는데 괜찮으리라 생각한다.

다음 포스팅부터는 논문의 본 내용을 다뤄보도록 하겠다.