| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 크롤링
- 리눅스
- Graph
- 베이지안
- uncertainty
- VAE
- Crawling
- 백준
- GNN
- 텍스트마이닝
- 코딩테스트
- AI
- 텍스트분석
- bayesian
- 파이썬
- 논문리뷰
- selenium
- PYTHON
- 강화학습
- 불확실성
- pytorch
- 우분투
- 빅데이터
- DATA
- R
- YarinGal
- pandas
- 알고리즘
- dropout
- 데이터분석
- Today
- Total
끄적거림
[논문 리뷰] On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification - 4.Aleatoric Uncertainty in Bayesian Classification 본문
[논문 리뷰] On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification - 4.Aleatoric Uncertainty in Bayesian Classification
Signing 2023. 4. 1. 00:55[논문 소개] On Uncertainty, Tempering, and Data Augmentation inBayesian Classification - 0.Abstract
[논문 리뷰] On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification - 1.Introduction
[논문 리뷰] On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification - 2.Related Work
[논문 리뷰] On Uncertainty, Tempering, and Data Augmentation in Bayesian Classification - 3.Background
이번 절에서는
(4.1섹션)에서 분류 문제에서의 Aleatoric Uncertainty 표현이 어떻게 되는지를 얘기하고,
(4.2섹션)에서는 tempering이 어떻게 Aleatoric Uncertainty를 줄일 수 있는지를,
(4.3섹션)에서는 수정된 Dirichlet 모델에서 tempering이 없는 Aleatoric Uncertainty를 어떻게 나타내는지를,
마지막으로 섹션5에서는 위의 내용들을 가지고 data augmentation이 어떻게 본 논문에서 주장하는 Aleatoric Uncertainty의 표현에 영향을 주는지를 보여준다.
4.1 How do we represent aleatoric uncertainty in classification?

(5)번식은 분류 문제에서 parameter $w$에 대한 BNN posterior이다.
$f_y(x,w)$ 부분을 input이 $x$에 따른 class $y$에 대한 softmax layer의 output으로 볼 수 있다.
uniform prior를 갖는 predicted class probabilities $f(x)$를 도입하면 아래와 같다.

이는 Dirichlet 분포임과 동일한데, 6번 식의 오른항을 보면, multi-normal model에서 uniform prior를 갖는 $f(x)$에 대한 Unnormalized posterior로 볼 수 있다.

이러한 사실에 근거하여, Dirichlet 분포를 conjugate하는 multi-nomial likelihood를 사용하면 6번 식을 7번 식으로 다시 쓸 수 있다.
---------------------------------------------------------
(23.05.22 업데이트)
Dirichlet분포는 Multi-nomial dist와 conjugate 관계에 있는데, Multi-nomial은 binomial 분포의 일반화된 버전이라고 보면 된다.
따라서 Multi Nomial dist는 2개가 아닌 k개의 class 중에서 1개가 뽑히는 이산형 확률분포이고, 이를 연속형 확률 분포로 변환한 것이 Dirichlet 분포라고 이해하면 된다.(느낌적 느낌으로 이해하면 된다. 정확한 내용은 아님)
Dirichlet 분포에서 1이 의미하는 것은 Dirichlet의 parameter을 의미한다.
K개의 class가 있다고 가정하고, 전부 동일한 가중치(uniform하게)를 주었다고 볼 수 있다.
전부 1인 상황에서 갑자기 (7)번 수식에서처럼 2로 변한 것은, 특정 class y에 대해 1개의 observation이 추가되었다고 보면 된다.
그렇기 때문에, observation으로 데이터 1개가 추가 되었다 = multi nomial dist가 추가되었다. = prior였던 dirichlet분포에 likelihood인 multi nomial분포를 곱하여, posterior인 dirichlet 분포가 업데이트(1에서 2로 변환)되었다고 볼 수 있다.
---------------------------------------------------------

8번 식은 BNN에서 분류문제에 대해 aleatoric uncertainty를 어떻게 추정하는지 보여주는 식이다.
만약 prior $p(w)$를 무시하고 uniform한 $f(x)$를 적용한다면, $(x,y)$에 대한 posterior는 $f(x) = Dir.(1,..,2,...,1)$이 되고, correct class에 대한 posterior mean은 $\frac{2}{C+1}$이 될 것이다.
예를 들어 100개의 class가 있는 데이터셋이 있으면, $2/101 \approx 2\%$라고 볼 수 있는 것이다.
prior $p(w)$가 non-trivial join prior dist.(=변수 간에 복잡한 관계가 존재하여 갖는 joint한 분포)라면, posterior는 더(or 덜) confidence할 것이다.
특히, $p(w) = N(0, \alpha^2 I)$처럼 간단한 prior를 사용했다면, 데이터의 label에 대한 노이즈를 고려하지 않은 것이다.
식 8번은 두가지 aleatoric uncertainty에 대한 posterior를 수정할 방법을 제안한다.
- Increasing the Dirichlet concentration for the observed class(=posterior tempering)
: 관찰한 class에 대해서는 Dirichlet 분포의 집중도가 상승 - Decreasing the concentration for the unobserved class(=noisy Dirichlet model)
: 관측하지 못한 class들에 대해서는 Dirichlet 분포의 집중도가 감소
해당 문단에서 말하고자 하는 것은 분류 문제에서 어떻게 aleatoric uncertainty를 나타내는가?였다. 저자는 Bayesian Rule에서 쓰이는 posterior 정의와 conjugate 관계인 Multi-nomial dist.와 Dirichlet dist.를 사용하여 posterior에 대한 분포를 나타냈고, 이를 통해 aleatoric uncertainty를 표현할 수 있다고 하였다.
정확히 어떻게 aleatoric uncertainty를 추정했는지 수식적으로 100% 이해하진 못했지만, 추정할 수 있는 방법이 있다는 점만 알아두고 넘어가자.
4.2 Likelihood tempering reduces aleatoric uncertainty
섹션3에서 보았던 tempered likelihood posterior는 BNN분류문제에서의 수식 (5)의 posterior를 아래 9번 식처럼 표현할 수있다.

9번식을 좀 더 풀어서 쓰면 아래 10번 식처럼 표현할 수 있다.
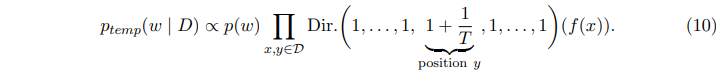
tempered posterior은 결국 일반적인 posterior와 비슷하지만, 각 input $x$에 대한 class $y$에 $1/T$만큼 더 count한 것으로 생각할 수 있다.
5번 수식과 비교 했을 때, $position ~ y$ 부분이 2였던 것이 $1 + \frac{1}{T}$ 로 변한것을 볼 수 있다.
한마디로, 특정 클래스 $y$에 대해 $1/T$만큼 한 번 더 더해줬다는 얘기이다.
따라서, tempering을 하게 되면 $position ~ y$에 대해 더 큰 값을 적용하는 것과 같다.
특히, prior $p(w)$는 $f(x)$에 대해 uniform dist.를 적용시켰다고 가정한다면, correct label에서 confidence는 tempered posterior의 평균은 $Expected~f_y(x) = \frac{1+1/T}{C+1/T} = \frac{T+1}{CT+1}$와 같을 것이다.
100 classes가 있는 dataset이고 $T=10^{-2}$이라면, confidence를 $50.5\%$ 를 얻을 수 있고, 이 것은 $2\%$보다 훨씬 더 높은 수치이다.
그에 따라, correct label에서의 confidence는 대폭 상승하며, incorrect label에서는 confidence가 더욱 낮아진다. 왜냐하면, class가 100개인 상황에서 일반적인 uniform dist.였다면 2%를 제외한 98%가 99개의 다른 class에 대해 할당이 될 것이고, dirichlet dist.이라면 correct label에 대해 50.5% confidence 얻는 반면, 나머지 99개의 incorrect label에 대해 50/99 정도의 confidence를 갖게하기 때문이다.
Tempering the Likelihood vs Tempering the Posterior
이전 연구에서는 보통 수식 (3)에서처럼의 likelihood를 tempering하는 것과 반대로 수식 (2)에서의 bayesian posterior 전체를 tempering하는 것을 연구한다.
Appendix C.2에서 나타나있듯이, 본 논문에서는 bayesian posterior을 tempering하는 것은 거의 항상 prior dist.를 변경하는 것과 likelihood를 tempering하는 것과 동일하다는 것을 보였다.
likelihood를 tempering하는 것이 posterior를 tempering하는 cold posterior effect와 동일함을 말하고 있다.
How should we think about tempering?
이전 연구에서는 posterior tempering이 베이지안 패러다임에서 크게 벗어나고 cold posterior effect가 매우 문제가 있다고 주장해왔다.
하지만, 본 논문에서는 likelihood tempering이 사실 Aleatoric uncertainty에 대한 논문에서의 가정을 설명하는데 좋은 방법이라고 소개한다.
관련되어, A STATISTICAL THEORY OF COLD POSTERIORS IN DEEP NEURAL NETWORKS 논문에서 cold posterior effect는 data curation을 일으킨다고 주장하고 있다.
한 예로, CIFAR-10과 ImageNet dataset은 비교적 매우 적은 label noise를 갖고 있기 때문에 조심스럽게 data curation을 한다.
그에 따라, low temperature를 갖는 tempered likelihood는 최적의 성능을 보여줄 수 있을 것이라 기대한다.
Bayesian deep learning and a probabilistic perspective of generalization (NIPS 2020) 논문에서도 posterior tempering을 observation model의 변화로 볼 수있다. -> 어떤 패러다임을 바꾼 것이다. + 모델을 보는 시각을 변화시켰다.
Is Tempered Likelihood a Valid Likelihood?
일반적인 베이지안 추론에서, 모델은 input 에 대한 조건부적인 label의 dist. $p(y|x)$이다.
How Good is the Bayes Posterior in Deep Neural Networks Really? 에서 tempered softmax likelihood는 class에 대한 확률이 1이 되지 않기 때문에 일반적으로 정확한 likelihood라고 할 수 없다고 주장한다.
그러나, $T<1$인 tempered softmax likelihood는 train data에서 한 번도 관측하지 않은 새로운 likelihood라고 설명할 수 있음을 보였다.
만약 그들이 이러한 설명을 올지 않다고 주장한다면, 이것은 모델에서 관측하지 않은 class를 포함하는 것이 모순됨을 설명하지 못하는 것이다.
게다가 수식 (10)번으로부터 우리는 논란의 여지 없이 완벽하게 multinomial 모델로써 사용하는 것이 tempered likelihood가 각 training datapoint에서 관찰되는 label의 $1/T$를 count하는 것임을 자연스럽게 생각해볼 수 있다.
4.3 Noisy Dirichlet model: changing the prior over class probabilities
수식 (10)에서 보았던 것처럼, likelihood tempering은 관찰된 class $y$에 대하여 Dirichlet dist.을 $2$에서 $1+1/T$로 올리면서 posterior confidence를 상승시킨다.
본 논문에서는 관측되지 않은 class의 집중도를 떨어뜨리면서 비슷한 효과를 입증했다.
(구체성을 위해 여기서는 모델의 confidence를 높이는 것에 대해 논의하지만, label noise의 레벨이 높을 것으로 예상되는 경우, 관찰되지 않은 class에 대한 concentration parameter를 늘림으로써 모델의 confidence를 동등하게 낮출 수 있다.)
그래서 조절 가능한 parameter인 $\alpha_{\epsilon}$을 추가한 $Noisy~Dirichlet$ 분포인 아래와 같은 식 (11)처럼 $p_{ND}$으로 나타낼 수 있다.

Noisy Dirichlet 모델은 Dirichlet-based gaussian processes for large-scale calibrated classification (NIPS 2018) 논문에 나왔던 것으로 Gaussian Process classification에 사용되었다.
본논문에서는, 예를 들어, class가 100개면 $\alpha_{\epsilon} = 10^{-2}$로 쓸 수 있고, expected confidence인 $Expected~f_y(x) = \frac{\alpha_{\epsilon}+1}{C_{\alpha_{\epsilon}} + 1} = 50.5%$이고 이것은 $T=10^{-2}$인 tempered likelihood와 같음을 알 수 있다.
Dirichlet과 multinomial dist.이 conjugate한 것을 사용하여, $p_{ND}$를 아래 수식 (12)처럼 다시 쓸 수 있다.

위 식에서 $q_{ND}(w)$는 y에 depend하지 않고, 학습 데이터의 class 중 하나의 confidence에 대한 predicted class 확률값이다.
Dangers of bayesian model averaging under covariate shift 논문에 나오는 $EmpCov$ prior도 y에 depend하지 않음을 밝히고 있다.
Noisy Dirichlet prior는 직관적이다. 어떤 면에서 그러냐면,
우리는 일단 모델이 한 class에 대해 높은 confidence를 갖기를 바라고, aleatoric uncertainty가 낮기를 바란다.
그와 동시에 input space의 모든 곳에서 aleatoric uncertainty가 낮기만을 바라는 것은 아니다.
training data에서 aleatoric uncertainty가 낮기를 바라면서, 모든 가능한 input이 높은 confidence를 갖기를 바라면 안된다.
섹션 6.3에서는 Dirichlet model이 cold posterior effect를 제거하는 것을 소개하고 있다.
tempering은 높은 성능을 내기에 필요하지 않다.
Gaussian Approximation
Dirichlet-based Gaussian Processes for Large-scale Calibrated Classification 논문에서는 Gaussian Process classification 쪽 내용에서 수식 (12)의 dist.에 대해 언급하지만 다른 목적으로 언급한다. : softmax likelihood를 근사하기 위한 regression likelihood를 만드는 것에 목적을 두고 있다.
해당 논문에서는 $Dir.(f(x))$를 class probability $f(x)$와 logit $z(x)$에 대한 independent Gaussian dist.를 사용하여 근사시킨다.

그리하여 나온 것이 $Noisy~Dirichlet~Gaussian$ 근사이다.
BNN에서 수식 (13)의 Gaussian approximation을 사용하기를 꺼려하고 바로 수식 (12)을 사용하길 바라지만, 실제 적용을 해보면 근사하는 방법(13)이 더 안정적인 결과를 얻을 수 있다.
게다가, 근사하는 방법(13)은 가우시안 모델의 logit $z(x)$의 space안에서 regression 문제를 푸는 것과 같다.
그에 따라 본 논문의 실험 부분에서는 $p_{NDG}$모델을 사용한다.
Visual comparison

- 왼쪽 그림은 이진분류 문제에서 standard soft max likelihood, temperd likelihood, noisy Dirichlet model를 사용하여 correct class $y$에 대한 confidence $f_y$의 posterior dist. CDF를 나타내고 있다.
$\{f(x)\}_{x \propto D}$에 대한 prior가 $x$에 대해 uniform과 independent함을 가정하였다.
tempering 방법과 noisy Dirichlet 방법은 standard softmax likelihood 방법보다 $f_y$ 예측값에 대해 더 높은 confidence를 보였다. - 중간 그림은 가장 효율적인 temperature를 나타내고 있다.
낮은 temperature가 더 높은 confidence prediction을 갖는다는 것이다. - 이와 비슷하게 오른쪽 그림은 $\alpha_{\epsilon}$의 값이 더 낮을수록 noisy Dirichlet 모델에서 더 높은 confidence를 보였다.
Gaussian approximation인 $NDG$는 noisy Dirichlet 모델의 CDF와 잘 맞는 경향이 있지만, 부드러운 느낌은 약하고 더 numerical sampling에 따르게 한다


