| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- AI
- selenium
- uncertainty
- 텍스트마이닝
- 우분투
- 강화학습
- Crawling
- 리눅스
- 빅데이터
- VAE
- dropout
- 크롤링
- 베이지안
- 텍스트분석
- 백준
- pandas
- GNN
- 코딩테스트
- PYTHON
- bayesian
- R
- 데이터분석
- 불확실성
- Graph
- 논문리뷰
- YarinGal
- pytorch
- 알고리즘
- 파이썬
- DATA
- Today
- Total
끄적거림
[논문 리뷰] Learning Transferable Graph Exploration - 3.Model 본문
[논문 리뷰] Learning Transferable Graph Exploration - 0.Abstract
[논문 리뷰] Learning Transferable Graph Exploration - 1.Introduction
[논문 리뷰] Learning Transferable Graph Exploration - 2.Problem Formulation
[논문 리뷰] Learning Transferable Graph Exploration - 3.Model
[논문 리뷰] Learning Transferable Graph Exploration - 4.Experiments - (1)Synthetic 2D Maze Exploration
[논문 리뷰] Learning Transferable Graph Exploration - 4.Experiments - (3)App Testing
[논문 리뷰] Learning Transferable Graph Exploration - 5.Related work & 6.Conclusion
Overview of the Framework
모든 step $t$에서 action policy $\pi(x|h_t;\theta_t)$를 학습하는 것을 목표로 할 것이다.
이 specific MDP의 objective fucntion은 다음과 같다.

기억해야할 것이, $\theta$를 매 time step마다 공유할 수 있고 모든 $t$에 대한 단일 policy $\pi(x|h_t, \theta)$를 학습한다.
그러나 finite horizon MDP에서는 매번 다른 time step $t$에서 다른 $\theta$를 사용하기 위해 효율적으로 찾는다.
본 논문에서는 단일 graph 구조의 environment에서의 효율적인 탐색 뿐 아니라,
보지 못한 graph에서의 재학습 혹은 fine-tuning과 같은 것 없이 사용할 수 있는 탐색 전략에 대한 generalization과 transferrability까지 관심 있는 것이다.
더 구체적으로 말하자면, $\mathbb{g}$를 graph 구조의 environment라고 표기해보자면, 본 논문에서는 아래의 meta-R/L 문제에 관심이 있는 것이다.

여기서 $\mathbb{D}$ 는 우리가 관심있어하는 graph 탐색 문제의 분포이고, 우리는 parameter들을 graph를 통해 공유한다.
학습이 이루어지고 난 후에, 학습된 policy는 같은 분포를 따르는 새로운 graph인 $\mathbb{g}^{\prime} ~ \mathbb{D}$를 parameter가 특정 $\mathbb{g}$에 연결되어 있지 않도록 generalize할 수 있다.
Graph Structured Agent and Exploration History
수식 (3)의 최적화 학습을 할 수 있게 하는 agent를 개발하기 위해서 가장 중요한 점은 모델이 다음의 것들을 수행할 수 있어야 한다.
- 효율적인 exploit과 graph의 구조를 잘 표현할 수 있어야 한다.
- 탐색의 기록을 통합하고 encoding 할 수 있어야 한다.
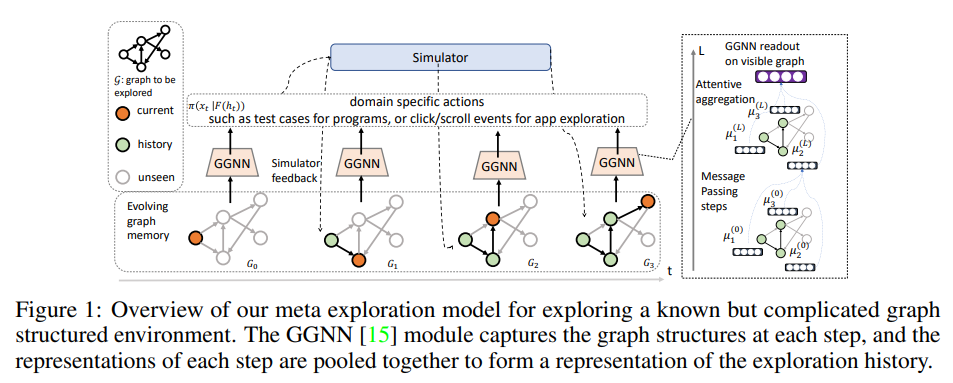
<그림 1>은 agent 구조의 전반적인 그림이다.
관측한 것들이 graph 구조를 띄기 때문에, 본 논문에서는 관측한 것들을 연속적인 vector space로 embeding시킨 변형된 Graph Neural Network(GNN)을 사용하였다.
즉, GNN을 이용하여 $g : (G, c) -> \mathbb{R}^d$를 수행했다.
이 내용은 node feature인 $\mu_v^{(0)}$를 초기화하는 것부터 시작이다. 구체적인 예를 들자면, 프로그램 분기에 대한 syntax 정보나 app screen feature 등이 있다.
또한 런타임 coverage 정보를 추가한 나머지 한 비트 $c_t(v)$를 포함한 feature를 padding한다.
이런 표현은 반복적인 메시지 전달 프로세스를 통해 업데이트 된다.

위 식(4)에서 $\mathbb{N}(v)$는 노드 $v$의 neighbor을 의미하고, $e_{uv}$는 edge $(u,v)$의 feature을 의미한다.
이 반복 프로세스는 $L$번의 iteration을 갖으면서, $L$-hop neighborhoods로부터의 정보를 취합한다.
function $f(.)$를 업데이트하기 위해 GGNN의 parametreization을 사용한다.
그래프 표현식$g(G, c)$을 얻기 위해서는 attention 기반 weghted-sum을 사용하여 최근 메세지 전달 단계으로부터 node embedding한 $\mu_v^{(L)}$을 aggregate한다.
탐색 history를 구하는 것은 특히 중요하다.
강화학습에서 다른 비슷한 많은 문제들처럼, 탐색 보상은 history를 고려할 때, 빠르게 "좋은"상태를 visit하는 그 한 번만 보상 받을 수 있는 것처럼, 항상 일정하다.
$h_t$를history에 위해 발전하는 graph 구조 memory로 취급한다.
전체 history의 표현은 단계별 표현을 집계하여 얻는다.
공식적으로, history $h_t$를 위한 representation function $F$를 다음과 같이 설계했다.

여기서 $g_x$는 action에 대한 encoder이고 대괄호$[.]$는 concatenation의 연산자이다.
function $F$는 다양한 형식을 취할 수 있는데 예를 들어서,
1) 가장 최근의 element
2) 혹은 $t$ step에 따른 auto-regressive aggregation
이다.
본 논문에서는 이에 대한 몇 가지 다른 설정을 탐색하고 auto-regressive $F$로 최고의 결과를 얻었다.(Appendix B.1)
history $h_t$의 encoding에 따라 조건화된 action policy $\pi(x_t|h_t) = \pi(x_t|F(h_t))$는 도메인의 특별한 NN으로 parameterized된다.
action이 프로그램 input으로 생성되는 프로그램 테스트에서, $\pi$는 RNN sequence decoer인 반면에 가능한 action의 유한 집합을 갖는 다른 문제에서는 MLP가 대신 사용된다.
Learning
이 agent를 학습하기 위해서, 동기화된 분산된 세팅에서 advantage actor critic 알고리즘을 적용한다.
32개의 분산된 actor을 사용하여 policy상의 궤적을 병렬로 수집하고, 이를 single machine으로 집계하여 parameter 업데이트를 진행한다.



