[논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 2.Related Work(1)

이전 글: 

2020/11/10 - [논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 1.Introduction

 

---

2. Related Work

본 논문에서 말하는 불확실성은 결국 분산으로 생각할 수 있다.

우리가 어떤 분포에서 분산을 알 수 있다면, 어느정도의 확률로 예측범위안에 들어올 것이다 를 알 수 있다.

이는 곧 신뢰구간과 비슷한 의미라고 생각하면 되겠다.

논문에서는 uncertainty를 sigma, variance 등과 같은 분산 혹은 어떤 분포로 혼용하여 사용하기도 한다.

 

기존의 Bayesian Deep Learning(이하 BDL)에서는 epistemic과 aleatoric 둘 중 하나만 측정하여 사용하는 것이 가능했었다고 한다.

 

여기서 BDL을 처음 접하는 사람은 그게 무엇인가 싶다.

관련 논문 : arxiv.org/pdf/1505.05424.pdf

 

weight distribution

나도 위의 논문을 읽어본 것은 아니지만 간단히 아는대로 적자면,

왼쪽 그림은 우리가 흔히 알고 있는 Neural Network 모델(이하 NN)이다.

 input으로 데이터가 들어오면, output으로 결과가 도출되며, 각 노드들에 적용되는 weight들은 고정된 상수값으로 정해져있고, 이 weight를 알기 위해 우리는 gradient 방법론을 사용하여 데이터에 알맞는 weight에 대한 근사값을 구한다.

이때 우리는 data에 대해서 분포를 적용한다.

 데이터가 어떤 분포를 갖을 것이고, 그 분포를 따르게 도와주는 절대적인 모수 weight가 존재할 것이라 믿는다.

가령 이런 것이다.

우리가 단순선형 회귀분석을 진행한다고 생각해보자.

단순선형 회귀분석 모델

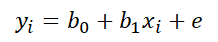
여기서 우리가 b0와 b1을 알기 위해서 보통 어떤 방법을 썼었는지 생각해보자.

MLE

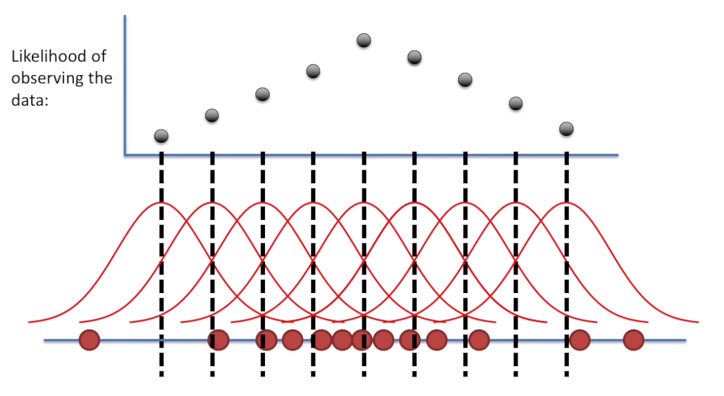
가능도가 최대가 되는 방향으로 weight를 추정하는 MLE 방법론을 사용했었다.

이러한 컨셉이 결정론적 세계관(deterministic)이다.

 

반면에, 베이지안 세계관은 그 근본이 다르다.

베이지안은 결정론적 세계관에서 적용되었던 데이터에 대한 분포를 데이터에 적용시키지 않고, weight에 적용시켰다.

발생할 수 있는 error를 weight에 적용시킨 것이다.(첫번째 그림 오른쪽 참고)

 

 

여기까지 간단한 BDL에 대해 개념만 잡고 가자.(관련 내용은 더 공부해서 포스팅할 예정)

 

 

 

 

 

 

2.1 Epistemic Uncertainty in Bayesian Deep Learning

 

 본 챕터에 들어가기 앞서, Dropout variational inference에 대해 알 필요가 있다. 해당 내용은 참고 논문의 핵심 내용이다.(참고 논문 : Dropout as a Bayesian) 이 논문도 나중에 다루겠지만 여기서는 핵심만 짚고 넘어가고자 한다.

 우리가 기존에 알고 있는 drop out은 regularization과 같은 과적합 방지 목적과 더불어 참여도가 낮은 노드들을 제거하여 모델의 복잡도를 낮추는데 있다.

Drop out

 dropout의 작동원리를 보면, 임의의 노드(뉴런)을 골라서 drop시킨 후 그것을 반복 시행하면서 더 좋은 성능을 내는 모델을 찾는다.

 이렇게 반복하면서 실제 분포에 근사시키는 과정을 몬테 카를로(Monte-Carlo) 근사라 하며, 이 과정에서 여러 weight들은 binary하게(실제로 1 또는 0 값만 갖는 것은 아니고, 0 또는 a 의 값으로 생각하면 되겠다.) 껐다 켜졌다를 반복하면서 특정 분포를 따르게 된다.

 이 때 발생하는 특정 분포가 각 weight에 대한 분포로 볼 수 있기 때문에, Dropout 방법론을 적용하여 베이지안 Network로 근사하여 변경할 수 있다.

 

밑의 수식은 이러한 내용을 포함하는 수식이며, Regression Task에서 해당 모델의 loss function에 해당한다.

 

Loss Function

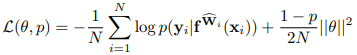
수식이 나와서 반감을 살 수도 있지만 하나씩 뜯어보면 사실 그렇게 어려운 수식은 아니다.

우변에서 첫번째 항은 negative log likelihood이며, 이는 아래의 수식처럼 근사될 수 있다.

log-likelihood 근사

 이것이 근사될 때 MSE항과 sigma항으로 분리될 수 있는데, 여기서의 sigma는 Aleatoric uncertainty(데이터 불확실성)가 되겠다.(sigma에 대한 언급은 다음 포스팅에 이어서 할 예정이다.) 여기서 MSE를 포함한 loglikelihood term이 Epistemic uncertainty(모델 불확실성)이 된다.

 따라서, 위의 loss function은 전체 모델에 대한 불확실성(epistemic + aleatoric)이 된다.

하지만 이것으로 두 uncertainty를 결합할 수 있는 것은 아니다. 단지 두 불확실성을 엮을 수 있는 기본 컨셉인 것이다.

 

 한 편,같은 이유로 Classification Task에서는 아래의 수식을 따른다.

 classification을 진행하기 바로 전에 어떤 수치를 정규화 및 확률화하기 위해서 보통 softmax function을 적용한다.

Monte Carlo integration이 적용되고, drop out으로써 적용되니 각각 나온 결과들을 평균 내주는 방법으로 y가 c로 분류될 확률값을 구할 수 있다.(여기서 T는 T번 sampling 했다는 것을 의미한다.)

 우리는 이에 대한 loss로써 entropy를 사용하곤 한다.

 

 

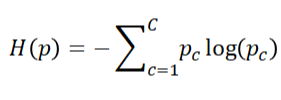
 마지막으로 Regression에서 Epistemic uncertainty(model)를 variance를 계산함으로써 확인할 수 있다.

variance as epistemic uncertainty

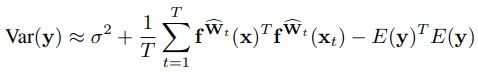
 여기서 첫 번째 항인 sigma^2항은 데이터로부터 나온 항이라 볼 수 있는데 나중에 나올 aleatoric uncertainty 파트에서 다룰 예정이다.

 첫 번째 항을 제외하고서는 우리가 흔히 알고 있는 분산의 공식(제곱의 평균 - 평균의 제곱, 제평평제: 학부시절 분산공식을 외우던 습관,,ㅎㅎ)과 유사함을 볼 수 있다.

 

이러한 Epistemic Uncertainty는 데이터를 더 많이 학습시킬수록 줄여나갈 수 있다고 말하고 있다.