| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DATA
- YarinGal
- 베이지안
- AI
- bayesian
- R
- pytorch
- PYTHON
- 불확실성
- 파이썬
- 텍스트마이닝
- 데이터분석
- VAE
- 강화학습
- 우분투
- Crawling
- selenium
- pandas
- 백준
- 리눅스
- 논문리뷰
- GNN
- 코딩테스트
- 알고리즘
- 빅데이터
- 텍스트분석
- dropout
- uncertainty
- 크롤링
- Graph
- Today
- Total
끄적거림
[논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 3.Combining Aleatoric and Epistemic Uncertainty in One Model(1) 본문
[논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 3.Combining Aleatoric and Epistemic Uncertainty in One Model(1)
Signing 2020. 11. 13. 15:43
논문을 이해하는 중에 오류가 있을 수 있습니다.
혹시 발견하시면 댓글로 알려주시면 감사하겠습니다 :)
3. Combining Aleatoric and Epistemic Uncertainty in One Model
이 절에서는 Bayesian Deep Learning에서 두 불확실성을 어떻게 결합했는지를 말하고 있다.
그 동안은 aleatoric이면 aleatoric, epistemic이면 epistemic. 이렇게 따로따로 모델링이 이뤄졌었다.
3.1 Combining Heteroscedastic Aleatoric Uncertainty and Epistemic Uncertainty
지난 번 포스팅에서 보았던 loss function을 다시 가져와보자.
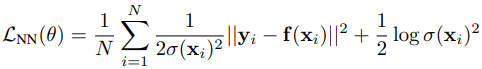
여기서 sigma함수는 각 x들에 대한 표준편차이자, 데이터 불확실성으로 작용했고, 이 loss function의 전반적인 식은 gaussian distribution의 pdf의 log를 취한 log-likelihood에서 나온 것임을 다시 한 번 기억하자.
위의 식에서는 Heteroscedastic Aleatoric Uncertainty만 반영된 형태였고, 우리는 이것을 weight의 distribution을 알 수 있는 Bayesian NN으로 바꾸길 바란다.
그렇게 되면 Aleatoric uncertainty와 Epistemic Uncertainty 모두 구할 수 있기 때문이다.(weight distribution을 알게된다면, 모델의 불확실성을 아는 것이기 때문에 Epistemic Uncertainty를 아는 것과 같다.)
본 논문에서는 weight distribution을 여러가지 방법으로 표현한다.
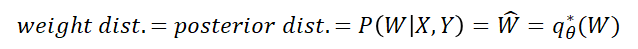
사실 이 모든 표현이 100% 일치하는 표현은 아니다. 대략적으로 비슷한 의미로 쓰이니 그렇게 알고 넘어가면 한다.
그래서 우리는 이 posterior dist.를 알아야 epistemic uncertainty를 구할 수 있는데 어떻게 구하냐면, 전 포스팅에서도 언급했던 2.1절에서 Epistemic uncertainty를 구하는 방법인 dropout variational inference 방법론을 이용할 것이다.

여기서, 우변은 모델 함수를 의미하며, x는 input, 좌변에서 y는 함수값, sigma^2는 분산으로 나타나는데, 가만보면 hat을 씌우고 있다.
알고있듯이 hat이 붙으면 추정치임과 동시에 기댓값으로도 활용할 수 있다.
기대값은 보통 불편추정량으로써 산술평균을 많이 사용하므로, 위에서의 좌변은 모두 평균치이다.
우선 평균을 내려면 여러 sample들이 필요한데 그 sample들은 dropout sampling에서 나온 것들일 것이다.
그래서, monte carlo dropout을 통해 일반적이었던 NN 모델이 BNN 모델로 추정되면 아래와 같이 기술 될 수 있다.
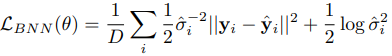
맨 위에서 보았던 식과의 차이점이라고 하면 무엇이 있을까?
바로
f(x_i) --> y^hat
sigma(x) --> sigma_hat
일 것이다.
이것이 dropout을 진행하면서 나온 sample들을 가지고 하나의 기댓값으로 추정했기 때문에 추정시킬 수 있었던 것이다.
BNN의 loss function을 살펴보면 지난번 포스팅에서도 언급했듯이 MSE term과 sigma term으로 분리하여 볼 수 있다.
이 논문에서는 각각을 잔차와 regularization term이라 보고 있다.
이 regularization term이 불확실성이 무한히 커지는 것을 막아주는 역할을 한다고 나와있다.
하지만, 우리는 이 식을 그대로 적용하기보단 아래의 식을 사용하는 편이 더 낫다.
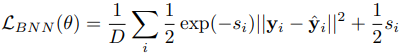
이 전의 식과 달라진 점은
sigma^hat --> s_i
로 바뀐 것이다.
여기서 s_i는 log(sigma^hat^2)이다. 즉, 기존 sigma에 log를 취한 것이다.
이렇게 해주는 이유는 분산인 sigma를 더욱 안정적이게 만들뿐만 아니라 N/0 꼴을 막기 위해서이다.(0으로 나눠지는 꼴)
그리하여, y pixel에서의 uncertainty를 구할 수 있는 방법은 아래와 같다.





