| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 파이썬
- 알고리즘
- YarinGal
- 불확실성
- AI
- 백준
- VAE
- 우분투
- 텍스트분석
- GNN
- selenium
- bayesian
- PYTHON
- R
- uncertainty
- 강화학습
- dropout
- Graph
- DATA
- 빅데이터
- Crawling
- 리눅스
- 데이터분석
- pandas
- 논문리뷰
- 크롤링
- 코딩테스트
- 텍스트마이닝
- pytorch
- 베이지안
- Today
- Total
끄적거림
[논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 3.Combining Aleatoric and Epistemic Uncertainty in One Model(2) 본문
[논문 리뷰] What uncertainties do we need in Bayesian deep learning for computer vision? - 3.Combining Aleatoric and Epistemic Uncertainty in One Model(2)
Signing 2020. 11. 14. 18:07
논문을 이해하는 중에 오류가 있을 수 있습니다.
혹시 발견하시면 댓글로 알려주시면 감사하겠습니다 :)
3. Combining Aleatoric and Epistemic Uncertainty in One Model
3.2 Heteroscedastic Uncertainty as Learned Loss Attenuation
이 절에서는 loss attenuation이라는 개념이 등장한다.
어려운 개념이 아니라 직관적이고 단순한 개념이니 한 번 살펴보도록 하자.
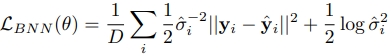
위의 식은 이전 포스팅에서 loss function이다.
여기서 첫 번째 항에서 sigma가 잔차의 분모와 regularization term으로 들어가 있기 때문에 sigma의 증감에 따라 전체 loss에 대한 영향도가 달라질 것이다.
잔차에 대해서는 불확실성(=sigma)이 가중치 역할을 하며 모델을 더욱 견고하게 만들어줄 것이고, 마지막 regularization항에서는 전체 loss에 대해 penalty를 부여하는 방향으로 작용할 것이다.
높은 불확실성을 갖는다고 판단되는 input에 대해서는 loss에 영향을 적게 줌으로써 학습하게 만든다.
이것의 의미는 불확실성이 높은 data는 학습 반영도를 낮춰서 학습을 진행하겠다는 의미이고, 더불어 불확실성이 낮은 data는 학습 반영도를 높게하여 학습을 진행하겠다는 의미이다.
즉, 불확실한 데이터에 대해서는 학습을 잘 하지 않게 하고, 확실한 데이터에 대해서는 잘 학습을 진행한다.
또한, 모델은 모든 pixel에 대해서는 높은 불확실성을 갖지 못하게 한다.
이것이 가능한 이유는 마지막 log(sigma^2)항 때문이다.
불확실성이 크면 log(sigma^2)항이 커지고, 결과적으로는 모델에 대해 패널티를 부여함으로써 모델이 불확실성이 높은 데이터에 대해서 무시할 수 있도록 한다.
반대로, 낮은 불확실성을 갖으면 잔차에 대한 기여도를 높게 만들기 때문에 모형에 패널티를 더 부여하는 셈이다.
따라서 잔차가 높은 지점에서는 불확실성을 낮게 예측하는 것을 방지하는 역할을 하는 것이다.
이런 것들을 loss attenuation이라고 한다.
3.3 Heteroscedastic Uncertainty in Classification Tasks
이제 classification task에 대해서 적용시켜보자.
logit을 사용하여 heteroscedastic regression에서 하던 것을 임시로 classification으로 적용시킬 수 있다.
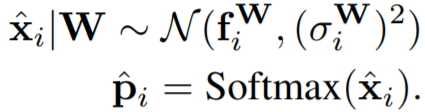
분류 문제에서 NN모델은 각 픽셀 i에 대해 softmax를 적용시킨 f_i를 예측한다.
여기서 f_i 값은 모델을 통해 나온 output이라 생각하면 된다.
우리는 이미 각 x들이 평균이 모델 함수값으로 나온 값이고, 분산이 sigma^2 행렬로 주어진 gaussian distribution을 따르는 것을 알고 있다.
여기서 분산 행렬은 diagonal matrix이며, 각 원소들은 softmax function이 적용되어 나온 값이라 보면 되므로 일종의 확률값으로 주어진다.
그렇다면 이 모델의 log-likelihood는 다음과 같을 것이다.
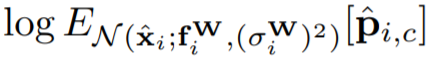
여기에 monte carlo integration과 마지막으로 softmax를 통과시켜 Gaussian distribution에 대해 근사시킬 수 있다.
그렇게 되면 아래와 같은 식이 나온다.

맨 아래의 loss function에서 중간의 sum(sigma라 부르는,,)에 대해서 잘 살펴보면 softmax임을 알 수 있다.
이것 역시 regression task에서처럼 loss attenuation을 적용시킬 수 있다.



